题目内容
已知方程 
表示焦点在y轴上的双曲线，则k的取值范围是（ ）
| A．3<k<9 | B．k>3 | C．k>9 | D．k<3 |
C
解析试题分析：根据双曲线方程的特点可知，方程 表示焦点在y轴上的双曲线，则说明而来原式变形为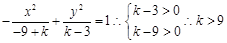
，故答案选C.
考点：本试题考查了双曲线的方程的表示。
点评：对于双曲线的方程的特点是等式左边是平方差，右边为1，同时分母中为正数，因此可知要使得焦点在x轴上，则必须保证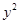
的系数为正，因此可知不等式表示的范围得到结论，属于基础题。
练习册系列答案
相关题目
，它的一个焦点为F1，则满足
为等边三角形的椭圆的离心率是（ ）
抛物线
的焦点到双曲线
的渐近线的距离为（ ）
A． | B． | C． | D． |
已知椭圆的长轴长是短轴长的
倍，则椭圆的离心率等于
A． | B． | C． | D． |
若双曲线
的左焦点在抛物线y2=2px的准线上，则p的值为（ ）
| A．2 | B．3 | C．4 | D．6 |
中心在坐标原点的椭圆，焦点在x轴上，焦距为4，离心率为
，则该椭圆的方程为
A． | B． | C． | D． |
如图，椭圆的中心在坐标原点0，顶点分别是A1, A2, B1, B2，焦点分别为F1 ,F2，延长B1F2 与A2B2交于P点，若
为钝角，则此椭圆的离心率的取值范围为
A．（0， ） | B．（，1） |
C．（0， ） | D．（ ，1） |
顶点在原点，且过点
的抛物线的标准方程是
A． | B． |
| C．或 | D． 或 |
已知点
是椭圆
上一点，
为椭圆的一个焦点，且
轴，
焦距，则椭圆的离心率是( )
A． | B． －1 | C． －1 | D．－ |