题目内容
如图，在⊙O中，弦CD垂直于直径AB，求证：| CB |
| CO |
| CD |
| CA |
分析：由已知中，弦CD垂直于直径AB，结合垂径定理，结合圆周角定理，我们易得△CAD∽△COB，再由相似三角形的性质，即可得到结论．
解答：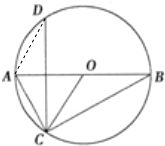
证明：连接AD，如图所示：
由垂径定理得：AD=AC
又∵OC=OB
∴∠ADC=∠OBC=∠ACD=∠OCB
∴△CAD∽△COB
∴
=
．
证明：连接AD，如图所示：由垂径定理得：AD=AC
又∵OC=OB
∴∠ADC=∠OBC=∠ACD=∠OCB
∴△CAD∽△COB
∴
| CB |
| CO |
| CD |
| CA |
点评：本题考查的知识点是垂径定理，相似三角形的判定与性质，圆周角定理，其中证明CAD∽△COB是解答本题的关键．
练习册系列答案
相关题目
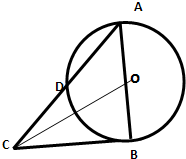如图，在⊙O中，AB为直径，AD为弦，过B点的切线与AD的延长线交于点C，且AD=DC，则sin∠ACO=
（2011•惠州模拟）如图，在⊙O中，AB为直径，AD为弦，过B点的切线与AD的延长线交于点C，且AD=DC，则sin∠BCO=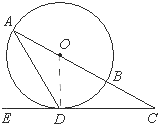
如图，在⊙O中，AB是直径，AD是弦，∠ADE=60°，∠C=30°．
如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分
