题目内容
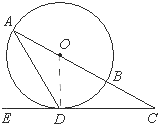 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.(1)判断直线CD是否是⊙O的切线,并说明理由;
(2)若CD=3
| 3 |
分析:(1)直线CD是⊙O的切线,理由如下:由题设条件知∠A=∠ADO=30°,从而得到∠ODC=90°,由此得到直线CD是⊙O的切线.
(2)由CD=3
,∠C=30°,CD是⊙O的切线,知tan30°=
=
,由此能求出BC.
(2)由CD=3
| 3 |
| OD | ||
3
|
| ||
| 3 |
解答:解:(1)直线CD是⊙O的切线,理由如下:
∵在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°,
∴∠A=∠ADO=30°,
∴∠ODC=90°,
∴直线CD是⊙O的切线.
(2)∵CD=3
,∠C=30°,CD是⊙O的切线,
∴tan30°=
=
,解得CD=3,
∴OB=2CD=6,
∴BC=6-OB=6-3=3.
∵在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°,
∴∠A=∠ADO=30°,
∴∠ODC=90°,
∴直线CD是⊙O的切线.
(2)∵CD=3
| 3 |
∴tan30°=
| OD | ||
3
|
| ||
| 3 |
∴OB=2CD=6,
∴BC=6-OB=6-3=3.
点评:本题考查圆的切线的判断,考查线段长的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
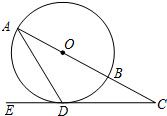 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30度.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30度.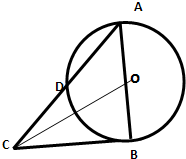 如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠ACO=
如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠ACO= 15、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是
15、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是
 (2011•惠州模拟)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠BCO=
(2011•惠州模拟)如图,在⊙O中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C,且AD=DC,则sin∠BCO= 如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分
如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分