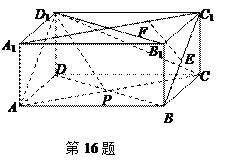题目内容
(本小题满分13分)如图,在梯形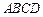 中,
中,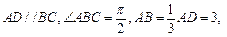

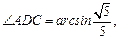
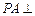 平面
平面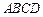 ,且
,且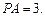
(1)求异面直线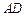 与
与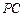 间的距离;
间的距离;
(2)求直线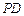 与平面
与平面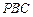 所成的角;
所成的角;
(3)已知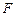 是线段
是线段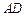 上的动点,若二面角
上的动点,若二面角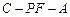 的
的
大小为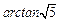 ,求AF.
,求AF.
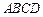 中,
中,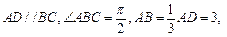

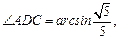
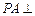 平面
平面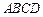 ,且
,且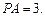
(1)求异面直线
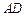 与
与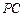 间的距离;
间的距离;(2)求直线
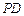 与平面
与平面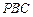 所成的角;
所成的角;(3)已知
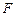 是线段
是线段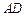 上的动点,若二面角
上的动点,若二面角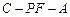 的
的大小为
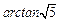 ,求AF.
,求AF.(1) 平面
平面
 平面
平面 ,故
,故 与
与 间的距离就是
间的距离就是

 到平面
到平面 的距离.取
的距离.取 中点
中点 ,连
,连 .
.

 平面
平面 又
又 平面
平面 故平面
故平面 平面
平面 由
由 得
得 平面
平面 ,故
,故 的长度是
的长度是 到平面
到平面 的距离,而
的距离,而 故
故 与
与 间的距离是
间的距离是
(2)由(1)知: 到平面
到平面 的距离即为
的距离即为 到平面
到平面 距离,故
距离,故 到平面
到平面 的距离是
的距离是 在
在 中:
中: 设直线
设直线 与平面
与平面 所成的角是
所成的角是 ,故
,故 ,∴直线
,∴直线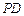 与平面
与平面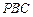 所成的角是
所成的角是
(3)作 于
于 ,作
,作 于
于 ,连
,连 .由
.由 得
得 则
则 证得
证得 可证
可证 得∠CKM是二面角
得∠CKM是二面角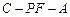 的平面角,所以
的平面角,所以 ,
, ,
,
∴ ,由
,由 ,
,
设 ,则
,则 ,
, ,由二面角
,由二面角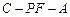 的平面角小于
的平面角小于 得
得 ,故取
,故取 ,即
,即 .
.
 平面
平面
 平面
平面 ,故
,故 与
与 间的距离就是
间的距离就是
 到平面
到平面 的距离.取
的距离.取 中点
中点 ,连
,连 .
.

 平面
平面 又
又 平面
平面 故平面
故平面 平面
平面 由
由 得
得 平面
平面 ,故
,故 的长度是
的长度是 到平面
到平面 的距离,而
的距离,而 故
故 与
与 间的距离是
间的距离是
(2)由(1)知:
 到平面
到平面 的距离即为
的距离即为 到平面
到平面 距离,故
距离,故 到平面
到平面 的距离是
的距离是 在
在 中:
中: 设直线
设直线 与平面
与平面 所成的角是
所成的角是 ,故
,故 ,∴直线
,∴直线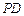 与平面
与平面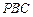 所成的角是
所成的角是
(3)作
 于
于 ,作
,作 于
于 ,连
,连 .由
.由 得
得 则
则 证得
证得 可证
可证 得∠CKM是二面角
得∠CKM是二面角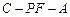 的平面角,所以
的平面角,所以 ,
, ,
,∴
 ,由
,由 ,
,设
 ,则
,则 ,
, ,由二面角
,由二面角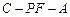 的平面角小于
的平面角小于 得
得 ,故取
,故取 ,即
,即 .
.
练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ). 
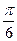



 ⊥平面
⊥平面 ,直线
,直线
 平面
平面 ,下面有三个命题:①
,下面有三个命题:①

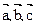 ,若
,若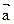 ∥
∥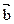 ,
,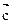 则
则 的底面是正方形,
的底面是正方形, ,点E在棱PB
,点E在棱PB 上
上 .(Ⅰ)求证:平面
.(Ⅰ)求证:平面 ;
; (Ⅱ)当
(Ⅱ)当 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.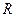 的球互相外切,且每个球都同时与另两个半径为
的球互相外切,且每个球都同时与另两个半径为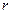 的球外切.如果这两个半径为
的球外切.如果这两个半径为