题目内容
13.设a,b,c是三个正实数,且a(a+b+c)=bc,则$\frac{a}{b+c}$的最大值为$\frac{\sqrt{2}-1}{2}$.分析 由已知条件可得a为方程x2+(b+c)x-bc=0的正根,求出a,再代入$\frac{a}{b+c}$变形化简利用基本不等式即可求出
解答 解:a(a+b+c)=bc,
∴a2+(b+c)a-bc=0,
∴a为方程x2+(b+c)x-bc=0的正根,
∴a=$\frac{-(b+c)+\sqrt{(b+c)^{2}+4bc}}{2}$,
∴$\frac{a}{b+c}$=$\frac{-(b+c)+\sqrt{(b+c)^{2}+4bc}}{2(b+c)}$=-$\frac{1}{2}$+$\frac{\sqrt{(b+c)^{2}+4bc}}{2(b+c)}$=-$\frac{1}{2}$+$\frac{1}{2}$$\sqrt{1+\frac{4bc}{(b+c)^{2}}}$=-$\frac{1}{2}$+$\frac{1}{2}$$\sqrt{1+\frac{4}{\frac{b}{c}+\frac{c}{b}+2}}$≤-$\frac{1}{2}$+$\frac{1}{2}$$\sqrt{1+\frac{4}{4}}$=$\frac{\sqrt{2}-1}{2}$,当且仅当b=c时取等号,
故答案为:$\frac{\sqrt{2}-1}{2}$,
点评 本题考查了基本不等式的应用,关键是正确的转化,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.若a+a-1=3,则a2+a-2的值为( )
| A. | 9 | B. | 7 | C. | 6 | D. | 4 |
1.已知函数y=Asin(ωx+ϕ)+m的最大值为4,最小值为0,最小正周期为π,直线$x=\frac{π}{6}$是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
| A. | $y=4sin(2x+\frac{π}{6})$ | B. | $y=-2sin(2x+\frac{π}{6})+2$ | C. | $y=-2sin(x+\frac{π}{3})+2$ | D. | $y=2sin(2x+\frac{π}{3})+2$ |
2.在等差数列{an}中,a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,类比上述性质,相应地在等比数列{bn}中,若b9=1,则成立的等式是( )
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
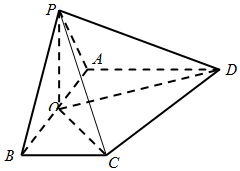 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3