题目内容
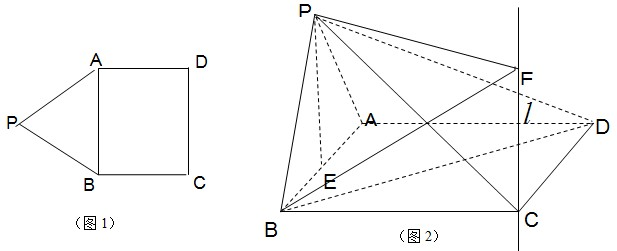
如图,过二面角αlβ内的一点P作PA⊥α,PB⊥β,A、B为垂足.已知PA=5,PB=8,AB=7,则此二面角的大小为 ;P点到棱l的距离d= .
解析:∵PA⊥α,PB⊥β,
∴PA⊥l,PB⊥l.?
∴l⊥平面ABP.?
设垂足为C,连结AC、BC,l⊥AC,l⊥BC.?
则∠ACB即为二面角αlβ的平面角.?
∵PA⊥α,PB⊥β,∴四边形APBC为圆内接四边形,PC为外接圆的直径.?
在△ABP中,由余弦定理,得?
cos∠APB=![]() ,?
,?
∴∠APB=60°.∴∠ACB=120°,?
即二面角的大小为120°.?
由正弦定理,PC=2R=![]() ,?
,?
即P点到棱l的距离![]() .
.
答案:120° ![]()

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
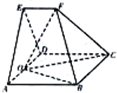 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,O是线段AD的中点,过E作直线l∥AB,F是直线l上一动点.
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,O是线段AD的中点,过E作直线l∥AB,F是直线l上一动点. (2013•四川)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点.
(2013•四川)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD的中点.