Question

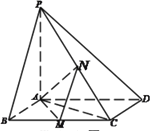
【题目】如图，在直三棱柱中，底面是等腰直角三角形， ，侧棱，D、E分别是与的中点，点E在平面ABD上的射影是的重心

(Ⅰ)求与平面ABD所成角的余弦值

(Ⅱ)求点到平面的距离

Answer 1

【答案】（Ⅰ）；（Ⅱ）.

【解析】试题分析：（Ⅰ）先利用线面角的定义找出线面角，再利用解直角三角形进行求解；（Ⅱ）先利用面面垂直的判定定理证明面面垂直，再利用利用面面垂直的性质作出线面垂直，得到点到平面的距离.

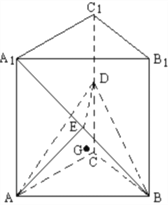
试题解析：（Ⅰ）连结，则是在的射影，即是与平面所成的角.设为中点，连结，∵分别是的中点，又平面，则为正方形，连接， 是的重心，且，在直角三角形中， ， ， ， ，

即

（Ⅱ） ，又，

即平面平面，作，垂足为，所以平面，即是到平面的距离，在三角形中， ，则

到平面的距离为。