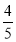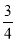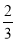题目内容
在平面直角坐标系中,O是坐标原点,两定点A,B满足| |=|
|=| |=
|= ·
· =2,则点集{P|
=2,则点集{P| =λ
=λ +μ
+μ ,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( ).
,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( ).
A.2 B.2
B.2 C.4
C.4 D.4
D.4
D
【解析】由| |=|
|=| |=
|= ·
· =2,知cos∠AOB=
=2,知cos∠AOB= ,又0≤∠AOB≤π,则
,又0≤∠AOB≤π,则
∠AOB= ,又A,B是两定点,可设A(
,又A,B是两定点,可设A( ,1),B(0,2),P(x,y),由
,1),B(0,2),P(x,y),由 =λ
=λ +μ
+μ ,可得
,可得 ⇒
⇒ 
因为|λ|+|μ|≤1,所以 +
+ ≤1,当
≤1,当
由可行域可得S0= ×2×
×2× =
= ,所以由对称性可知点P所表示的区域面积S=4S0=4
,所以由对称性可知点P所表示的区域面积S=4S0=4 ,故选D.
,故选D.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目