题目内容
已知：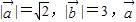
和
的夹角为45°，求：（1）当向量
与λ
的夹角为钝角时，λ的取值范围；（2）当λ=-2时，向量
与λ
的夹角的余弦值．
【答案】分析：（1）由已知中
与
的夹角为钝角，知
且
，根据
和
的夹角为45°，可构造一个关于λ的不等式，解不等式即可得到λ的取值范围；
（2）求出当λ=-2时，向量
与λ
的模及数量积，代入向量夹角公式，即可求出向量
与λ
的夹角的余弦值．
解答：解：（1）∵
与
的夹角为钝角，知
且
由
得3λ2+11λ+3＜0
解得
；
当
时，由
与
不共线知
，解得λ=t=-1（1舍去）
所以λ的取值范围是
或
；
（2）当λ=-2时|
+λ
|=|
-2
|=
|λ
+
|=|-2
+
|=
=
（
+λ
）•（λ
+
）=（
-2
）•（-2
+
）=-2
2-2
2+5
=-7
所以 cos
点评：本题考查的知识点是平面向量的综合应用，其中（1）中易忽略向量
与λ
反向的情况，而错解为
．
与
的夹角为钝角，知
且
，根据
和
的夹角为45°，可构造一个关于λ的不等式，解不等式即可得到λ的取值范围；（2）求出当λ=-2时，向量
与λ
的模及数量积，代入向量夹角公式，即可求出向量
与λ
的夹角的余弦值．解答：解：（1）∵
与
的夹角为钝角，知
且
由
得3λ2+11λ+3＜0解得
；当
时，由
与
不共线知
，解得λ=t=-1（1舍去）所以λ的取值范围是
或
；（2）当λ=-2时|
+λ
|=|
-2
|=
|λ
+
|=|-2
+
|=
=
（
+λ
）•（λ
+
）=（
-2
）•（-2
+
）=-2
2-2
2+5
=-7所以 cos
点评：本题考查的知识点是平面向量的综合应用，其中（1）中易忽略向量
与λ
反向的情况，而错解为
． 
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
|=
，|
|=3，
和
的夹角为45°，若向量（λ
+
）⊥（
+λ
），则实数λ的值为 ．
|=
，|
|=3，
和
的夹角为45°，求当向量
+λ
与λ
+
的夹角为锐角时，λ的取值范围．
•
=4
，|
|=4，
和
的夹角为45°，则|
|为（ ）
•
=4
，|
|=4，
和
的夹角为45°，则|
|为（ ）