题目内容
已知sin(x+π)=- ,计算:
,计算:
(I)sin(5π-x)-cos(x- );
);
(II)sin( +x)-tan(
+x)-tan( +x).
+x).
解:(Ⅰ)∵sin(x+π)=- ,∴sinx=
,∴sinx= ,cosx=±
,cosx=± ,∴sin(5π-x)-cos(x-
,∴sin(5π-x)-cos(x- )
)
=sinx+cosx. 当cosx= 时,所求的式子等于
时,所求的式子等于 ,当cosx=-
,当cosx=- 时,所求的式子等于
时,所求的式子等于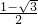 ,
,
(II) sin( +x)-tan(
+x)-tan( +x)=cosx-
+x)=cosx-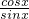 =cosx(1-
=cosx(1-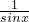 )=-cosx=±
)=-cosx=± =±
=± .
.
分析:(Ⅰ) 由诱导公式可得sinx= ,cosx=±
,cosx=± ,由sin(5π-x)-cos(x-
,由sin(5π-x)-cos(x- )=sinx+cosx 求出结果.
)=sinx+cosx 求出结果.
(II)利用诱导公式可得 sin( +x)-tan(
+x)-tan( +x)=cosx-
+x)=cosx-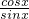 =cosx(1-
=cosx(1-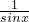 )=-cosx=±
)=-cosx=± .
.
点评:本题考查同角三角函数的基本关系,诱导公式的应用,注意三角函数符号的选取.
 ,∴sinx=
,∴sinx= ,cosx=±
,cosx=± ,∴sin(5π-x)-cos(x-
,∴sin(5π-x)-cos(x- )
) =sinx+cosx. 当cosx=
 时,所求的式子等于
时,所求的式子等于 ,当cosx=-
,当cosx=- 时,所求的式子等于
时,所求的式子等于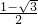 ,
,(II) sin(
 +x)-tan(
+x)-tan( +x)=cosx-
+x)=cosx-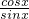 =cosx(1-
=cosx(1-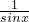 )=-cosx=±
)=-cosx=± =±
=± .
.分析:(Ⅰ) 由诱导公式可得sinx=
 ,cosx=±
,cosx=± ,由sin(5π-x)-cos(x-
,由sin(5π-x)-cos(x- )=sinx+cosx 求出结果.
)=sinx+cosx 求出结果.(II)利用诱导公式可得 sin(
 +x)-tan(
+x)-tan( +x)=cosx-
+x)=cosx-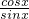 =cosx(1-
=cosx(1-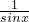 )=-cosx=±
)=-cosx=± .
.点评:本题考查同角三角函数的基本关系,诱导公式的应用,注意三角函数符号的选取.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目