题目内容
设A、B是x轴上的两点,点P的横坐标是2,且|PA|=|PB|,直线AP的方程为x-y+1=0,则直线PB的方程是( )A.x+y-5=0 B.2x-y-1=0 C.2x-y-4=0 D.2x+y-7=0
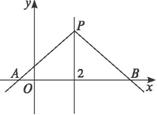
解法一:直线PA、PB关于直线x=2对称,则直线PA、PB的倾斜角互补,斜率互为相反数.由k PA=1,则kPB=-1,排除B、C、D,故选A. 解法二:由于P在直线x-y+1=0上,则当x=2时,y=3即P(2,3).如图所示,由PA与PB关于直线x=2对称可得PA、PB的倾斜角互补,斜率互为相反数,∵kPA=1,∴kPB=-1.∴直线PB的方程是y-3=-1×(x-2),即x+y-5=0.故选A. 答案:A
 练习册系列答案
练习册系列答案

每时每刻快乐优加系列答案
孟建平培优一号系列答案
孟建平毕业总复习系列答案
密解1对1系列答案
名师导练系列答案
名师讲堂单元同步学练测系列答案
名师面对面中考满分特训方案系列答案
名师名卷单元月考期中期末系列答案
初中总复习教学指南系列答案
相关题目