题目内容
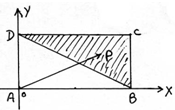 (2012•芜湖二模)设长方形ABCD边长分别是AD=1,AB=2(如图所示),点P在△BCD内部和边界上运动,设
(2012•芜湖二模)设长方形ABCD边长分别是AD=1,AB=2(如图所示),点P在△BCD内部和边界上运动,设| AP |
| AB |
| AD |
分析:根据已知构造出阴影部分中的点满足的约束条件
,进而根据点P在△BCD内部和边界上运动,设
=α•
+β•
,找出x,y与α,β的关系,将可行域中各角点坐标代入比照后,求出目标函数的最值,即可得到答案.
|
| AP |
| AB |
| AD |
解答:解:∵长方形ABCD边长分别是AD=1,AB=2
阴影部分内的点满足
设P(x,y),则
=(x,y)=α•(2,0)+β•(0,1)=(2α,β)
即:x=2α,y=β
因此
当x=2,y=0,即α=1,β=0时,α+2β=1;
当x=2,y=1,即α=1,β=1时,α+2β=3;
当x=0,y=1,即α=0,β=1时,α+2β=2;
α+2β∈[1,3]
故选B
阴影部分内的点满足
|
设P(x,y),则
| AP |
即:x=2α,y=β
因此
|
当x=2,y=0,即α=1,β=0时,α+2β=1;
当x=2,y=1,即α=1,β=1时,α+2β=3;
当x=0,y=1,即α=0,β=1时,α+2β=2;
α+2β∈[1,3]
故选B
点评:本题考查的知识点是简单线性规划的应用,其中根据已知构造出满足条件的约束条件是解答本题的关键.

练习册系列答案
相关题目
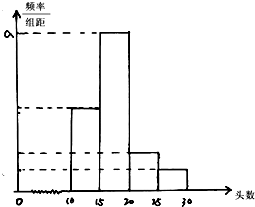 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: