Question

已知数列{a_n}中,a₁=t(t≠0,且t≠1),a₂=t²,且当x=t时,函数f(x)= (a_n-a_n-1)x²-(a_n+1-a_n)x(n≥2)取得极值.

(1)求证:数列{a_n+1-a_n}是等比数列.

(2)若b_n=a_nln|a_n|(n∈N^*)，求数列{b_n}的前n项和S_n.

(3)当t=-时，数列{b_n}中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由.

Answer 1

(1)证明：由f′(t)=0,得(a_n-a_n-1)t=a_n+1-a_n(n≥2).?

又a₂-a₁=t²-t=t(t-1),?

∵t≠0且t≠1,∴a₂-a₁≠0.?

∴=t.

∴数列{a_n+1-a_n}是首项为t²-t,公比为t的等比数列.                                               ?

(2)解：由(1)知a_n+1-a_n=(t²-t)t^n-1(t≠1且t≠0),

即a_n+1-a_n=tⁿ⁺¹-tⁿ,?

∴a_n-a_n-1=tⁿ-t^n-1,?

_an-1-a_n-2=t^n-1-t^n-2,?

……?

a₂-a₁=t²-t,?

上面n-1个等式相加并整理得?

a_n=tⁿ(T≠0且T=1),                                                                                                 ?

b_n=a_nlg|a_n|=tⁿ·lg|tⁿ|=ntⁿlg|t|,?

S_n=(t+2·t²+3·t³+…+n·tⁿ)lg|t|,?

tS_n=［t²+2·t³+…+(n-1)tⁿ+ntⁿ⁺¹］lg|t|?,?

两式相减,(1-t)S_n=(t+t²+…+tⁿ-ntⁿ⁺¹)g|t|?,

整理得S_n=［-］lg|t|.                                                                 ?

(3)解：因为t=-，即-1＜t＜0,所以?              

当n为偶数时，b_n=ntⁿlg|t|＜0,?

当n为奇数时，b_n=ntⁿlg|t|＞0,?

所以最大项必为奇数项，?

设最大项为b_2k+1,则有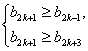 即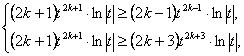

整理得                                                                                   ?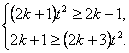

将t²=代入上式，解得≤k≤.?

∵k∈N^*,?

∴k=2,即数列{b_n}中的最大项是第5项.