题目内容
设D、E、F分别是△ABC的三边BC、CA、AB上的点且
=2
,
=2
,
=2
,则
+
+
与
( )
| BD |
| DC |
| EA |
| CE |
| FB |
| AF |
| AD |
| BE |
| CF |
| BC |
分析:根据平面向量基本定理和向量的线性运算,将
、
、
分别用
、
、
或其相反向量的线性组合来表示,再加得到
+
+
=
,由此即可得到本题答案.
| AD |
| BE |
| CF |
| AB |
| AC |
| BC |
| AD |
| BE |
| CF |
| 1 |
| 3 |
| BC |
解答:解:∵
=2
,
=
-
,
=
-
∴
-
=2(
-
),可得
=
+
同理可得
=
+
,
=
+
∴
+
+
=
+
+(
+
)+(
+
)
=(
+
)+(
+
)+(
+
)=
由此可得:
+
+
与
平行且同向
故选:A
| BD |
| DC |
| BD |
| AD |
| AB |
| DC |
| AC |
| AD |
∴
| AD |
| AB |
| AC |
| AD |
| AD |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
同理可得
| BE |
| 2 |
| 3 |
| BC |
| 1 |
| 3 |
| BA |
| CF |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
∴
| AD |
| BE |
| CF |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| BC |
| 1 |
| 3 |
| BA |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| CB |
=(
| 2 |
| 3 |
| AC |
| 2 |
| 3 |
| CA |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| BA |
| 2 |
| 3 |
| BC |
| 1 |
| 3 |
| CB |
| 1 |
| 3 |
| BC |
由此可得:
| AD |
| BE |
| CF |
| BC |
故选:A
点评:本题给出三角形ABC三边上的三等分点,求向量
+
+
与
的关系,着重考查了平面向量基本定理和向量的线性运算法则等知识,属于基础题.
| AD |
| BE |
| CF |
| BC |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设D、E、F分别是△ABC的三边BC、CA、AB上的点,且
=2
,
=2
,
=2
,则
+
+
与
( )
| DC |
| BD |
| CE |
| EA |
| AF |
| FB |
| AD |
| BE |
| CF |
| BC |
| A、反向平行 |
| B、同向平行 |
| C、互相垂直 |
| D、既不平行也不垂直 |
 设D,E,F分别是△ABC的边BC,CA,AB上的点,且
设D,E,F分别是△ABC的边BC,CA,AB上的点,且 =2
=2 ,
,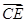 =2
=2 ,
, =2
=2 ,则
,则 +
+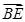 +
+ 与
与 ( )
( )