题目内容

1．若函数f（x）=3sin（ωx+φ）-1对任意的x都有f（x）=f（4-x）恒成立，则f（2）的值是（　　）
A．-2B．4C．2或-4D．-2或4

分析 利用已知条件求出函数的对称轴，通过函数的解析式，求解f（2）的值．

解答 解：∵函数f（x）=3sin（ωx+φ）-1对任意的x都有f（x）=f（4-x）恒成立，
可得函数的对称轴为：x=2，故函数f（2）是函数的最值，
可得f（2）=±3-1．f（2）的值是2或-4．
故选：C．

点评 本题主要考查三角函数的对称轴的问题．注意正余弦函数在其对称轴上取最值，是中档题．

练习册系列答案
相关题目
11．已知$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，|$\overrightarrow{c}$|=2，则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值为$\frac{\sqrt{2}}{4}$．
12．写出下列随机变量ξ可能取的值，并说明随机变量ξ=4所表示的随机试验的结果．
（1）从10张已编号的卡片（编号从1号到10号）中任取2张（一次性取出），被取出的卡片的较大编号为ξ；
（2）某足球队在点球大战中5次点球射进的球数为ξ
9．二项式（x-2y）7的展开式中，所有项系数绝对值之和等于37．
16．函数f（x）=3sin（x+$\frac{π}{6}$）+$\sqrt{3}$sin（$\frac{π}{3}$-x）的最大值是（　　）
A．3B．6C．$\sqrt{3}$D．2$\sqrt{3}$
6．某工厂实施煤改电工程防治雾霾，欲拆除高为AB的烟囱，测绘人员取与烟囱底部B在同一水平面内的两个观测点C，D，测得∠BCD=75°，∠BDC=60°，CD=40米，并在点C处的正上方E处观测顶部A的仰角为30°，且CE=1米，则烟囱高AB=1+20$\sqrt{2}$米．
13．已知正项数列{an}的前n项和为Sn，且Sn=$\frac{{a}_{n}^{2}+3{a}_{n}+2}{6}$．
（1）求数列{an}的通项公式；
（2）若a2=4a1，bn=$\frac{3}{{a}_{n}•{a}_{n+1}}$，求数列{bn}的前n项和Tn＜$\frac{15}{16}$时自然数n的取值范围．
10．已知集合A={2a，3}，B={a，b}，若A∩B={$\frac{1}{4}$}，则A∪B={-2，$\frac{1}{4}$，3}．
7．一个三棱锥的三视图如图所示，则该三棱锥的表面积为（　　）
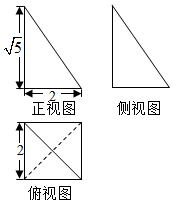
A．8+$\sqrt{14}$B．8+2$\sqrt{14}$C．2+2$\sqrt{5}$+$\sqrt{14}$D．16+2$\sqrt{14}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网