题目内容
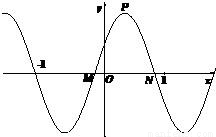
如图，函数f（x）在点P处的切线方程为y=-2x+9，则f（4）+f′（4）=-1
-1
．分析：根据导数的几何意义知，函数y=f（x）的图象在点P处的切线的斜率就是函数y=f（x）在该点的导数值，可求得f′（4），再根据切点的双重性，即切点既在曲线上又在切线上，可求得f（4），从而求出所求．
解答：解：根据图象知，函数y=f（x）的图象与在点P处的切线交于点P，
f（4）=-8+9=1，
f′（4）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（4）=-2；
则f（4）+f'（4）的值是-1
故答案为：-1
f（4）=-8+9=1，
f′（4）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（4）=-2；
则f（4）+f'（4）的值是-1
故答案为：-1
点评：本题主要考查了利用导数研究曲线上某点切线方程，以及导数的几何意义，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
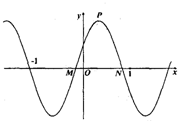已知函数
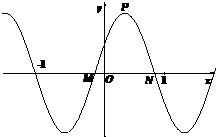
已知函数
，如图，函数f（x）在[-1，1]上的图象与x轴的交点从左到右分别为M，N，图象的最高点为P，则
的夹角的余弦值是（ ）
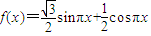，x∈R．
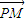与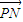
的夹角的余弦．