题目内容
己知△ABC的周长为9,且sinA:sinB:sinC=3:2:4,则cosC的值为( )A.

B.

C.

D.

【答案】分析:由题意利用正弦定理可得可得a=3、b=2、c=4,再由余弦定理可得 cosC=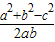 的值.
的值.
解答:解:由题意利用正弦定理可得三角形三边之比为a:b:c=3:2:4,再根据△ABC的周长为9,可得a=3、b=2、c=4.
再由余弦定理可得 cosC=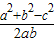 =
=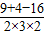 =-
=- ,
,
故选A.
点评:本题主要考查正弦定理和余弦定理的应用,求得a=3、b=2、c=4,是解题的关键,属于中档题.
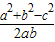 的值.
的值.解答:解:由题意利用正弦定理可得三角形三边之比为a:b:c=3:2:4,再根据△ABC的周长为9,可得a=3、b=2、c=4.
再由余弦定理可得 cosC=
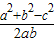 =
=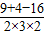 =-
=- ,
,故选A.
点评:本题主要考查正弦定理和余弦定理的应用,求得a=3、b=2、c=4,是解题的关键,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目