题目内容
如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=
。
(1)求四棱锥S-ABCD的体积；
(2)求证：面SAB⊥面SBC；
(3)求SC与底面ABCD所成角的正切值。
。(1)求四棱锥S-ABCD的体积；
(2)求证：面SAB⊥面SBC；
(3)求SC与底面ABCD所成角的正切值。
解：（1）
；
（2）∵SA⊥面ABCD，BC
面ABCD，
∴SA⊥BC，
又∵AB⊥BC，SA∩AB=A，
∴BC⊥面SAB，
又BC
面SBC，
∴面SAB⊥面SBC。
（3）连结AC，则∠SCA就是SC与底面ABCD所成的角，
在三角形SCA中，SA=1，AC=
，
∴
。
；（2）∵SA⊥面ABCD，BC
面ABCD，∴SA⊥BC，
又∵AB⊥BC，SA∩AB=A，
∴BC⊥面SAB，
又BC
面SBC，∴面SAB⊥面SBC。
（3）连结AC，则∠SCA就是SC与底面ABCD所成的角，
在三角形SCA中，SA=1，AC=
， ∴
。
练习册系列答案
名校课堂系列答案
相关题目
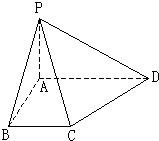如图，在底面是直角梯形的四棱锥P-ABCD中，AD∥BC，∠ABC=90°，且
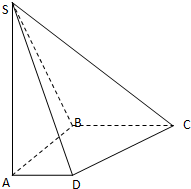如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=
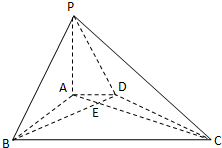如图，在底面是直角梯形的四棱锥 P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4．AD=2，AB=
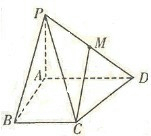如图，在底面是直角梯形的四棱锥P-ABCD中，∠DAB=90°，PA⊥平面 ABCD，PA=AB=BC=1，AD=2，M为PD中点．
如图，在底面是直角梯形的四棱锥S-ABCD中，已知∠ABC=90°，SA⊥平面ABCD，AB=BC=2，AD=1．