题目内容
已知抛物线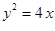 ,过
,过 轴上一点
轴上一点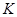 的直线与抛物线交于点
的直线与抛物线交于点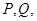 两点。
两点。
证明,存在唯一一点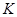 ,使得
,使得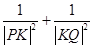 为常数,并确定
为常数,并确定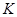 点的坐标。
点的坐标。
 时,
时, 为定值,此时
为定值,此时 。
。
解析试题分析:设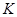 (
( ),过
),过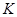 点直线方程为
点直线方程为 ,交抛物线于
,交抛物线于 联立方程组
联立方程组
由韦达定理得 …5分
…5分
使用, 7分
7分
即 , 12分
, 12分
所以, 时,
时, 为定值,此时
为定值,此时 。 17分
。 17分
考点:直线与抛物线的位置关系,两点间的距离公式。
点评:中档题,涉及直线与圆锥曲线位置关系问题,往往通过联立方程组,应用韦达定理,简化解题过程 。

练习册系列答案
相关题目
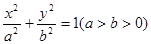 的离心率为
的离心率为 ,
,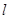 :y=x+2与原点为圆心,以椭圆C的短轴长为直
:y=x+2与原点为圆心,以椭圆C的短轴长为直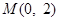 的直线
的直线 与椭圆
与椭圆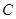 交于
交于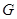 ,
,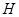 两点.设直线
两点.设直线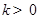 ,在
,在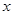 轴上是否存在点
轴上是否存在点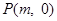 ,使得
,使得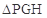 是以GH为底边的等腰三角形. 如果存在,求出实数
是以GH为底边的等腰三角形. 如果存在,求出实数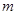 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.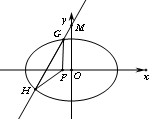
 中,点
中,点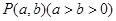 为动点,
为动点,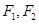 分别为椭圆
分别为椭圆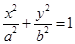 的左右焦点.已知△
的左右焦点.已知△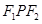 为等腰三角形.(1)求椭圆的离心率
为等腰三角形.(1)求椭圆的离心率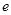 ;(2)设直线
;(2)设直线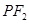 与椭圆相交于
与椭圆相交于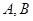 两点,
两点,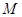 是直线
是直线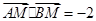 ,求点
,求点
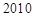 年
年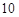 月
月 日
日 时
时 分
分 秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约
秒“嫦娥二号”探月卫星由长征三号丙运载火箭送入近地点高度约 公里、远地点高度约
公里、远地点高度约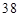 万公里的直接奔月椭圆(地球球心
万公里的直接奔月椭圆(地球球心 为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面
为一个焦点)轨道Ⅰ飞行。当卫星到达月球附近的特定位置时,实施近月制动及轨道调整,卫星变轨进入远月面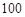 公里、近月面
公里、近月面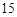 公里(月球球心
公里(月球球心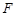 为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以
为一个焦点)的椭圆轨道Ⅱ绕月飞行,之后卫星再次择机变轨进入以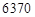 公里,月球半径约为
公里,月球半径约为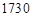 公里。
公里。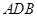 为半圆,
为半圆, 为半圆直径,
为半圆直径,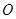 为半圆圆心,且
为半圆圆心,且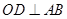 ,
,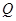 为线段
为线段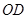 的中点,已知
的中点,已知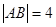 ,曲线
,曲线 过
过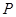 在曲线
在曲线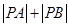 的值不变.
的值不变. 的直线
的直线 与曲线
与曲线 两点,与
两点,与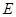 点,
点,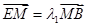 ,
,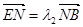 证明:
证明: 为定值.
为定值.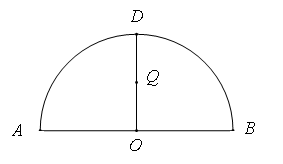
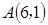 作直线与双曲线
作直线与双曲线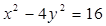 相交于两点
相交于两点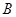 、
、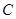 ,且
,且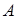 为线段
为线段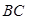 的中点,求这条直线的方程.
的中点,求这条直线的方程.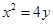 的焦点F的直线
的焦点F的直线 与抛物线相交于A,B两点。
与抛物线相交于A,B两点。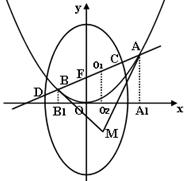
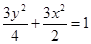 的交点为C、D,是否存在直线
的交点为C、D,是否存在直线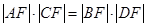 ,若存在,求出直线
,若存在,求出直线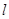 与抛物线
与抛物线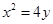 相切于点
相切于点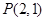 )且与
)且与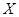 轴交于点
轴交于点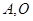 为坐标原点,定点B的坐标为
为坐标原点,定点B的坐标为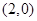 .
.
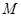 满足
满足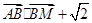 |
|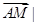 =
= ,求点
,求点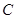 .
. 的直线
的直线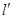 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹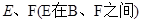 ,试求
,试求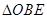 与
与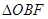 面积之比的取值范围.
面积之比的取值范围.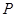 是直角坐标平面内的动点,点
是直角坐标平面内的动点,点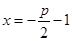 (
(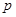 是正常数)的距离为
是正常数)的距离为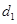 ,到点
,到点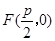 的距离为
的距离为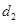 ,且
,且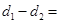 1.
1. 过点F且与曲线C交于不同两点A、B,分别过A、B点作直线
过点F且与曲线C交于不同两点A、B,分别过A、B点作直线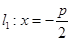 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为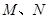 ,求证
,求证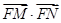 =
= ;
;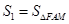 ,
,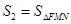 ,
,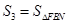
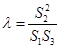 ,求
,求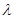 的值.
的值.