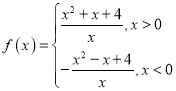题目内容
【题目】某农产品从5月1日起开始上市，通过市场调查，得到该农产品种植成本Q（单位：元/
）与上市时间t（单位：天）的数据如下表：
t | 50 | 110 | 250 |
Q | 150 | 108 | 150 |
（1）根据上表数据，从下列函数中选取一个函数描述该农产品种植成本Q与上市时间t的变化关系，并求出函数关系式：
，
，
，
.
（2）利用你选取的函数，求该农产品种植成本最低时的上市时间及最低种植成本.
【答案】（1）
；（2）该农产品种植成本最低时的上市时间为150天，最低种植成本为100元/（
）.
【解析】
（1）根据数据变化规律确实
，代入数据计算得到答案.
（2）化简得到
，根据二次函数单调性得到答案.
（1）由题表中提供的数据可知，描述该农产品种植成本Q与上市时间t的变化关系的函数不可能是常函数，因此用函数
，
，
中的任何一个进行描述时都应有
，而此时上述三个函数均为单调函数，这与表格中所提供的数据不符，所以应选取函数进行描述.
将题表所提供的三组数据分别代入
，得
解得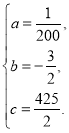
所以描述该求产品种植成本Q与上时间t的变化关系的函数为.
（2）
，
当
时，Q取得最小值，即
.
所以该农产品种植成本最低时的上市时间为150天，最低种植成本为100元/（）.
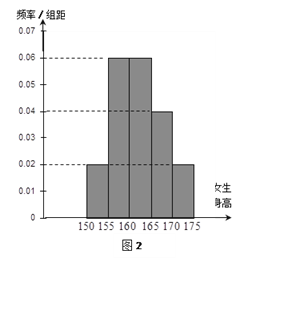
【题目】某学校为调查高三年级学生的身高情况，按随机抽样的方法抽取80名学生，得到男生身高情况的频率分布直方图（图1）和女生身高情况的频率分布直方图（图2）.已知图1中身高在170～175cm的男生人数有16人
.
(1)根据频率分布直方图，完成下列的
列联表，并判断能有多大（百分比）的把握认为“身高与性别有关”？
|
| 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(2)在上述80名学生中，从身高在170-175cm之间的学生按男、女性别分层抽样的方法，抽出5人，从这5人中选派3人当旗手，求3人中恰好有一名女生的概率.
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
参考公式及参考数据如下：
