题目内容
△ABC内接于⊙O:x2+y2=1(O为坐标原点),且3| OA |
| OB |
| OC |
(1)求△AOC的面积;
(2)若
| OA |
| OC |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
分析:(1)利用向量加法的平行四边形法则及三角形的面积公式求出△AOC的面积
(2)分别利用向量的数量积的坐标形式及模夹角形式的公式列出方程求出cos(θ-
),利用三角函数的平方关系求出sin(θ-
)
将角θ用角θ-
与角
表示,利用和角公式求出sinθ.
(2)分别利用向量的数量积的坐标形式及模夹角形式的公式列出方程求出cos(θ-
| π |
| 4 |
| π |
| 4 |
将角θ用角θ-
| π |
| 4 |
| π |
| 4 |
解答:解:(1)∵3
+4
+5
=0
∴3
+4
=-5
据向量加法的平行四边形法则得sin∠AOC=
,cos∠AOC=-
∴△AOC的面积=
OA•OC•sin∠AOC=
(2)∵
•
=(1,0)•(cos(θ-
),sin(θ-
))=cos(θ-
)
∵
•
=
||
|cos∠AOC═-
∴cos(θ-
)=-
∵θ∈(-
,0)
∴θ-
∈(-π,-
)
∴sin(θ-
)=-
∴sinθ=sin[(θ-
)+
]=sin(θ-
)cos
+cos(θ-
)sin
=-
| OA |
| OB |
| OC |
∴3
| OA |
| OB |
| OC |
据向量加法的平行四边形法则得sin∠AOC=
| 4 |
| 5 |
| 3 |
| 5 |
∴△AOC的面积=
| 1 |
| 2 |
| 2 |
| 5 |
(2)∵
| OA |
| OC |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∵
| OA |
| OC |
| |OA |
| OC |
| 3 |
| 5 |
∴cos(θ-
| π |
| 4 |
| 3 |
| 5 |
∵θ∈(-
| 3π |
| 4 |
∴θ-
| π |
| 4 |
| π |
| 4 |
∴sin(θ-
| π |
| 4 |
| 4 |
| 5 |
∴sinθ=sin[(θ-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
7
| ||
| 10 |
点评:本题是向量三角结合的题目,考查向量的数量积公式;三角函数的诱导公式;三角函数的和角公式;及凑角能力.

练习册系列答案
相关题目
 12、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于
12、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于
 14、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是
14、如图所示.△ABC内接于⊙O,若∠OAB=28°,则∠C的大小是
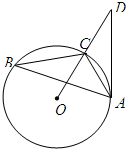 (2011•广州模拟)(几何证明选讲选做题)
(2011•广州模拟)(几何证明选讲选做题)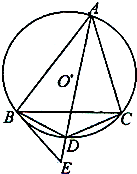 (2011•太原模拟)如图,△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,BE是切线,AD的延长线交BE于E,连接BD、CD.
(2011•太原模拟)如图,△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,BE是切线,AD的延长线交BE于E,连接BD、CD.