题目内容
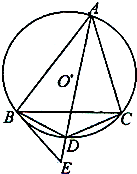（2011•太原模拟）如图，△ABC内接于⊙O，AD平分∠BAC，交⊙O于点D，BE是切线，AD的延长线交BE于E，连接BD、CD．（1）求证：BD平分∠CBE；
（2）求证：AB•BE=AE•DC．
分析：（1）利用AD平分∠BAC，可得弧BD=弧DC，BD=DC，从而可得∠CBD=∠BCD，即可证得BD平分∠CBE；
（2）证明△ABE∽△BDE，将比例式转化为等积式，利用BD=DC，可得结论．
（2）证明△ABE∽△BDE，将比例式转化为等积式，利用BD=DC，可得结论．
解答：证明：（1）∵AD平分∠BAC，∴弧BD=弧DC，BD=DC
∴∠CBD=∠BCD
∴∠BED=∠CBD
∴BD平分∠CBE；
（2）∵BE是切线，
∴∠EBD=∠BAD
∵∠E=∠E
∴△ABE∽△BDE
∴
=
∴AB×BE=AE×BD
∵BD=DC
∴AB•BE=AE•DC．
∴∠CBD=∠BCD
∴∠BED=∠CBD
∴BD平分∠CBE；
（2）∵BE是切线，
∴∠EBD=∠BAD
∵∠E=∠E
∴△ABE∽△BDE
∴
| AB |
| BD |
| AE |
| BE |
∴AB×BE=AE×BD
∵BD=DC
∴AB•BE=AE•DC．
点评：本题考查圆的切线的性质，考查三角形的相似，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目