题目内容
正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S-ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
分析:由动点P在正四棱锥的表面上运动,并且总保持PE⊥AC,故P点落在过E点且于AC垂直的平面上,根据线面平行的判定定理,找到满足条件的P点轨迹,解三角形可得答案.
解答: 解:连接AC,BD交于点O,连接SO,则SO⊥平面ABCD
解:连接AC,BD交于点O,连接SO,则SO⊥平面ABCD
由AC?平面ABCD,故SO⊥AC
取SC中点F和CD中点G,连接GE交AC于H
则H为OC的中点,故FH∥SO,
则FH⊥AC
又由GE∥BD,BD⊥AC得GE⊥AC
∵GE∩FH=H,GE,FH?平面FGE
∴AC⊥平面FGE
故当P∈平面FGE时,总有PE⊥AC,
故动点P的轨迹即为△FGE的周长
又∵正四棱锥S-ABCD的底面边长为2,高为2,
故SO=2,BD=2
则GE=
,SB=
则FE=FG=
故△FGE的周长为
+
故选D
 解:连接AC,BD交于点O,连接SO,则SO⊥平面ABCD
解:连接AC,BD交于点O,连接SO,则SO⊥平面ABCD由AC?平面ABCD,故SO⊥AC
取SC中点F和CD中点G,连接GE交AC于H
则H为OC的中点,故FH∥SO,
则FH⊥AC
又由GE∥BD,BD⊥AC得GE⊥AC
∵GE∩FH=H,GE,FH?平面FGE
∴AC⊥平面FGE
故当P∈平面FGE时,总有PE⊥AC,
故动点P的轨迹即为△FGE的周长
又∵正四棱锥S-ABCD的底面边长为2,高为2,
故SO=2,BD=2
| 2 |
则GE=
| 2 |
| 6 |
则FE=FG=
| ||
| 2 |
故△FGE的周长为
| 2 |
| 6 |
故选D
点评:本题考查的知识点是线面垂直的判定及性质,其中根据已知分析出P点落在过E点且于AC垂直的平面上,进而给出添加辅助线的方法是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
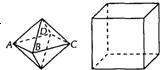
 9、两相同的正四棱锥组成左图所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
9、两相同的正四棱锥组成左图所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
 两个相同的正四棱锥组成如图所示的几何体,可放入棱
两个相同的正四棱锥组成如图所示的几何体,可放入棱