题目内容
设a为锐角,若cos(a+
)=
,则sin(2a+
)的值为______.
| π |
| 6 |
| 4 |
| 5 |
| π |
| 12 |
∵a为锐角,cos(a+
)=
,
∴a+
也是锐角,且sin(a+
)=
=
∴cosa=cos[(a+
)-
]=
cos
+
sin
=
sina=sin[(a+
)-
]=
cos
-
sin
=
由此可得sin2a=2sinacosa=
,cos2a=cos2a-sin2a=
又∵sin
=sin(
-
)=
,cos
=cos(
-
)=
∴sin(2a+
)=sin2acos
+cosasin
=
•
+
•
=
故答案为:
| π |
| 6 |
| 4 |
| 5 |
∴a+
| π |
| 6 |
| π |
| 6 |
1-cos2(a+
|
| 3 |
| 5 |
∴cosa=cos[(a+
| π |
| 6 |
| π |
| 6 |
| 4 |
| 5 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 6 |
4
| ||
| 10 |
sina=sin[(a+
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 6 |
| 4 |
| 5 |
| π |
| 6 |
3
| ||
| 10 |
由此可得sin2a=2sinacosa=
24-7
| ||
| 50 |
7+24
| ||
| 50 |
又∵sin
| π |
| 12 |
| π |
| 3 |
| π |
| 4 |
| ||||
| 4 |
| π |
| 12 |
| π |
| 3 |
| π |
| 4 |
| ||||
| 4 |
∴sin(2a+
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
24-7
| ||
| 50 |
| ||||
| 4 |
7+24
| ||
| 50 |
| ||||
| 4 |
17
| ||
| 50 |
故答案为:
17
| ||
| 50 |

练习册系列答案
相关题目
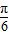 )=
)= ,则sin(2a+
,则sin(2a+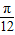 )的值为 .
)的值为 .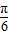 )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 . )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 . )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 .