题目内容
 (2012•海淀区一模)如图,以△ABC的边AB为直径的半圆交AC于点D,交BC于点E,EF⊥AB于点F,AF=3BF,BE=2EC=2,那么∠CDE=
(2012•海淀区一模)如图,以△ABC的边AB为直径的半圆交AC于点D,交BC于点E,EF⊥AB于点F,AF=3BF,BE=2EC=2,那么∠CDE=60°
60°
,CD=3
| ||
| 13 |
3
| ||
| 13 |
分析:如图所示,设圆心为点O,半径为R,连接OE,AE.利用已知AF=3FB,AF+FB=2R,可得FB=
R,又EF⊥AB,可得OE=EB,即△OEB为等边三角形,从而利用圆内接四边形的性质即可得出∠CDE的大小;也可求出AE.进而求出AC,再利用割线定理即可得出CD.
| 1 |
| 2 |
解答:解:如图所示,设圆心为点O,半径为R,连接OE,AE.
由AB为⊙O的直径,∴∠AEB=90°,∴AE⊥CE.
∵AF=3FB,AF+FB=2R,
∴FB=
R,又EF⊥AB,∴OE=EB,即△OEB为等边三角形.
∴∠ABE=60°.
∴∠CDE=∠ABE=60°;
∴AE=BEtan60°=2
.
在Rt△ACE,AC=
=
=
.
由割线定理可得:CD•CA=CE•CB,
∴CD=
=
.
故答案为60°;
.

由AB为⊙O的直径,∴∠AEB=90°,∴AE⊥CE.
∵AF=3FB,AF+FB=2R,
∴FB=
| 1 |
| 2 |
∴∠ABE=60°.
∴∠CDE=∠ABE=60°;
∴AE=BEtan60°=2
| 3 |
在Rt△ACE,AC=
| AE2+CE2 |
(2
|
| 13 |
由割线定理可得:CD•CA=CE•CB,
∴CD=
| 1×3 | ||
|
3
| ||
| 13 |
故答案为60°;
3
| ||
| 13 |
点评:本题综合考查了圆的性质、等边三角形的判定与性质、割线定理等基础知识,考查了推理能力和计算能力.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
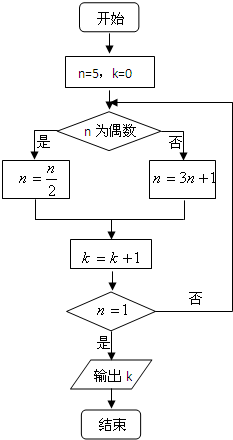 (2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )
(2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )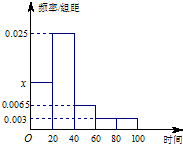 (2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].