题目内容
6.已知三个点A(0,0),B(2,0),C(4,2),则△ABC的外心的纵坐标是3.分析 设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,由点A(0,0),B(2,0),C(4,2),列出方程组,能求出△ABC的外心的纵坐标.
解答 解:设△ABC外接圆方程为x2+y2+Dx+Ey+F=0,
∵点A(0,0),B(2,0),C(4,2),
∴$\left\{\begin{array}{l}{F=0}\\{4+2D+F=0}\\{20+4D+2E+F=0}\end{array}\right.$,
解得D=-2,E=-6,F=0,
∴△ABC外接圆方程为x2+y2-2x-6y=0.
∴△ABC外接圆的圆心为(1,3),
∴△ABC的外心的纵坐标是3.
故答案为:3.
点评 本题考查三角形外心纵坐标的求法,是基础题,解题时要认真审题,注意待定系数法的合理运用.

练习册系列答案
相关题目
11.过点A(0,3),B(7,0)的直线l1与过点C(2,1),D(3,k+1)的直线l2互相垂直,则实数k的值为( )
| A. | $\frac{3}{7}$ | B. | -$\frac{3}{7}$ | C. | -$\frac{7}{3}$ | D. | $\frac{7}{3}$ |
 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, ,
,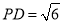 ,
, 为
为 与
与 的交点,
的交点, 为棱
为棱 上一点.
上一点.
 平面
平面 ;
; 平面
平面 ,求三棱锥
,求三棱锥 的体积.
的体积. 在区间(0,1)内的零点个数是( )
在区间(0,1)内的零点个数是( ) ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为 ,
,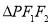 是以
是以 为底边的等腰三角形,若
为底边的等腰三角形,若 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.