题目内容
已知函数f(x)= x3
x3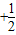 ax2+bx+c在x1处取得极大值,在x2处取得极小值,满足x1∈(-1,0),x2∈(0,1),则
ax2+bx+c在x1处取得极大值,在x2处取得极小值,满足x1∈(-1,0),x2∈(0,1),则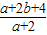 的取值范围是( )
的取值范围是( )A.(0,2)
B.(1,3)
C.[0,3]
D.[1,3]
【答案】分析:据极大值点左边导数为正右边导数为负,极小值点左边导数为负右边导数为正得a,b的约束条件,据线性规划求出最值.
解答: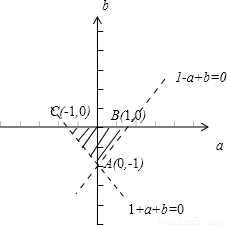 解:∵f(x)=
解:∵f(x)= x3
x3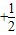 ax2+bx+c,
ax2+bx+c,
∴f′(x)=x2+ax+b
∵函数f(x)在区间(-1,0)内取得极大值,在区间(0,1)内取得极小值,
∴f′(x)=x2+ax+b=0在(-1,0)和(0,1)内各有一个根,
f′(0)<0,f′(-1)>0,f′(1)>0
即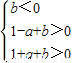 ,
,
在aOb坐标系中画出其表示的区域,如图,
∵A(0,-1),B(1,0),C(-1,0),
∴把A(0,-1)代入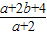 ,得到:
,得到: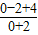 =1;
=1;
把B(1,0)代入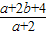 ,得到:
,得到: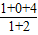 =
= ;
;
把C(-1,0)代入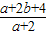 ,得到:
,得到: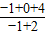 =3.
=3.
∴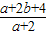 的取值范围是(1,3).
的取值范围是(1,3).
故选B.
点评:本题考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力,解题时要认真审题,仔细解答.
解答:
 解:∵f(x)=
解:∵f(x)= x3
x3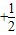 ax2+bx+c,
ax2+bx+c,∴f′(x)=x2+ax+b
∵函数f(x)在区间(-1,0)内取得极大值,在区间(0,1)内取得极小值,
∴f′(x)=x2+ax+b=0在(-1,0)和(0,1)内各有一个根,
f′(0)<0,f′(-1)>0,f′(1)>0
即
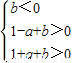 ,
,在aOb坐标系中画出其表示的区域,如图,
∵A(0,-1),B(1,0),C(-1,0),
∴把A(0,-1)代入
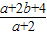 ,得到:
,得到: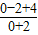 =1;
=1;把B(1,0)代入
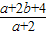 ,得到:
,得到: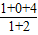 =
= ;
;把C(-1,0)代入
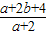 ,得到:
,得到: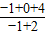 =3.
=3.∴
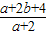 的取值范围是(1,3).
的取值范围是(1,3).故选B.
点评:本题考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|