题目内容
在椭圆
=1(a＞b＞0)的第一象限的
上求一点P,使四边形OAPB的面积最大,并求最大面积.
解析:如图,将四边形OAPB分割成△OAP与△OPB,则P点纵坐标为△OAP的OA边上的高,P点横坐标为△OPB的OB边上的高.
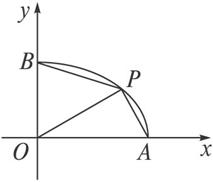
解:设P(acosθ,bsinθ),S四边形OAPB=S△OAP+S△OPB=absinθ+
abcosθ
=
ab(sinθ+cosθ)=
absin(
+θ).
当θ=
时,四边形OAPB面积最大,最大面积为
ab,此时,P点坐标为(
a,
b).
练习册系列答案
相关题目
=1(a＞b＞0)的第一象限的
上求一点P,使四边形OAPB的面积最大,并求最大面积.
=1(a＞b＞0)的左准线上,过点P且方向为a=(2,-5)的光线经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( )
B.
C.
D.
+
=1(a＞b＞0)上,焦点三角形PF1F2的内切圆的圆心为I,则点I分∠F1PF2的平分线AP(点A在F1F2上)所成的比是
B.
C.
D.
+
=1 (a＞b＞0)上,F1、F2为椭圆的两个焦点，求|PF1|·|PF2|的取值范围.
+
=1 (a＞b＞0)上,F1、F2为椭圆的两个焦点，求|PF1|·|PF2|的取值范围.