题目内容
(本小题满分14分)已知函数 的图象过点
的图象过点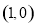 .
.
(1)求 的解析式;
的解析式;
(2)若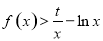 (
(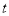 为实数)恒成立,求
为实数)恒成立,求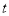 的取值范围;
的取值范围;
(3)当 时,讨论
时,讨论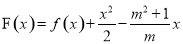 在区间
在区间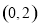 上极值点的个数.
上极值点的个数.
(1)f(x)=lnx;
(2)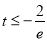 ;
;
(3)当m=1时,函数F(x)在(0,2)无极值点;当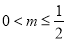 或m≥2时,F(x)有1个极值点;当
或m≥2时,F(x)有1个极值点;当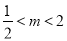 且m≠1时,F(x)有2个极值点.
且m≠1时,F(x)有2个极值点.
【解析】
试题分析:(1)函数 的图象过定点(1,0) 1分
的图象过定点(1,0) 1分
把点(1,0)代入 得
得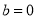
 f(x)=lnx 2分
f(x)=lnx 2分
(2)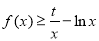 恒成立,即
恒成立,即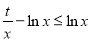 恒成立,得
恒成立,得

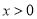

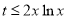 3分
3分
令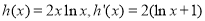 4分
4分
当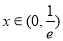 时,
时,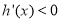 ,所以
,所以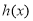 在
在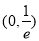 为减函数 5分
为减函数 5分
当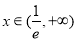 时,
时, ,所以
,所以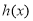 在
在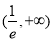 为增函数 6分
为增函数 6分
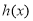 的最小值为
的最小值为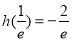
故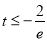 7分
7分
(3)由(1)知: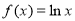

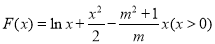
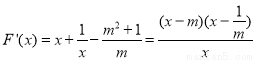
又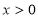 ,由F′(x)=0得,
,由F′(x)=0得,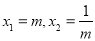 9分
9分
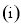 当
当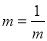 时,得m=1,F′(x)≥0,F(x)在(0,2)为增函数,无极值点 10分
时,得m=1,F′(x)≥0,F(x)在(0,2)为增函数,无极值点 10分
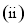 当
当 且
且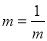 时,得
时,得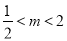 且m≠1,
且m≠1,
根据x,F(x),F′(x)的变化情况检验,可知F(x)有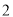 个极值点 12分
个极值点 12分
 当
当 或
或 时,得
时,得 或m≥2.
或m≥2.
根据x,F(x),F′(x)的变化情况检验,可知F(x)有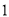 个极值点 13分
个极值点 13分
综上,当m=1时,函数F(x)在(0,2)无极值点;当 或m≥2时,F(x)有1个极值点;当
或m≥2时,F(x)有1个极值点;当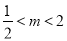 且m≠1时,F(x)有2个极值点. 14分
且m≠1时,F(x)有2个极值点. 14分
考点:考查了函数的解析式,利用导数研究函数的最值,极值问题.

练习册系列答案
相关题目
 ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( ) B.4 C.3 D.
B.4 C.3 D.
 解集是空集,则实数
解集是空集,则实数 的取值范围是_________.
的取值范围是_________.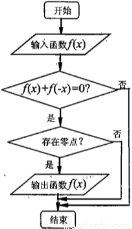
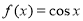 B.
B.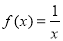
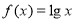 D.
D.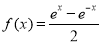
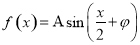 (
( ,
,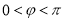 )的最大值是
)的最大值是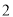 ,且
,且 .
.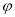 的值;
的值;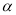 ,
,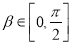 ,
,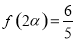 ,
,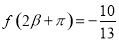 ,求
,求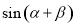 的值.
的值. ,
, ,
, ,
, ,满足
,满足 ,
,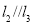 ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )

 与
与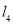 既不垂直也不平行
既不垂直也不平行  与
与 的位置关系不确定
的位置关系不确定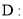
 ,令点集
,令点集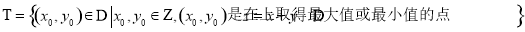 ,则
,则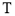 中的点共确定__________条不同的直线.
中的点共确定__________条不同的直线.