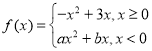题目内容
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)最小值为3,最大值为7;(3)
;(2)最小值为3,最大值为7;(3)![]() .
.
【解析】
(1)待定系数法求解析式,可设函数的解析式为![]() ,又由
,又由![]() ,即
,即![]()
![]() ,分析可得
,分析可得![]() 、
、![]() 的值,将
的值,将![]() 、
、![]() 的值代入函数的解析式,即可得答案;
的值代入函数的解析式,即可得答案;
(2)根据题意,分析可得![]() ,结合
,结合![]() 的范围分析可得答案;
的范围分析可得答案;
(3)根据题意,由![]() 的解析式可得
的解析式可得![]() ,由基本不等式的性质分析可得
,由基本不等式的性质分析可得![]() ,据此分析可得答案.
,据此分析可得答案.
解:(1)根据题意,二次函数![]() 满足
满足![]() ,设其解析式为
,设其解析式为![]() ,
,
又由![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() ,
,
则![]() ;
;
(2)由(1)的结论,![]() ,
,
又![]() ,
,
当![]() 时,
时,![]() 取得最小值,且其最小值
取得最小值,且其最小值![]() ,
,
当![]() 时,
时,![]() 取得最大值,且其最大值
取得最大值,且其最大值![]() ;
;
故![]() 在
在![]() 上的最小值为3,最大值为7;
上的最小值为3,最大值为7;
(3)由(1)的结论,![]() ,则
,则![]() ,
,
又由![]() ,则
,则![]() ,当且仅当x=2等号成立
,当且仅当x=2等号成立
若![]() 恒成立,必有
恒成立,必有![]() ,解可得
,解可得![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】行了一次水平测试。用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究。经统计成绩的分组及各组的频数如下:![]() ,2;
,2;![]() ,3;
,3;![]() ,10;
,10;![]() ,15;
,15;![]() ,12;
,12;![]() ,8.
,8.
(Ⅰ)频率分布表
分组 | 频数 | 频率 |
| 2 | |
| 3 | |
| 10 | |
| 15 | |
| 12 | |
| 8 | |
合计 | 50 |
频率分布直方图为
(Ⅰ)完成样本的频率分布表;画出频率分直方图;
(Ⅱ)估计成绩在85分以下的学生比例;
(Ⅲ)请你根据以上信息去估计样本的众数、中位数、平均数.(精确到0.01)