题目内容
(2012•道里区三模)下列命题中正确的是( )
分析:A:利用奇函数的定义域必须关于原点对称,可得A不正确.
B:由x∈[0,
]得出
-2x的取值范围,再利用正弦函数的单调性进行判断.
C:利用诱导公式化简函数的解析式为 y=2sin(
-x),再根据正弦函数的值域求出它的最小值.
D:利用三角函数的恒等变换化简函数的解析式为
sin2πx,从而得到函数的周期性和奇偶性.
B:由x∈[0,
| π |
| 3 |
| π |
| 6 |
C:利用诱导公式化简函数的解析式为 y=2sin(
| π |
| 3 |
D:利用三角函数的恒等变换化简函数的解析式为
| 1 |
| 2 |
解答:解:对于A:由于函数y=sinx,x∈[0,2π]的定义域不关于原点对称,故它不奇函数,故A不正确.
B:由x∈[0,
]得出
-2x∈(-
,
),正弦函数f(x)=sinx在(-
,
)上是增函数,
函数y=2sin(
-2x)在区间[0,
]上是单调递减的,故B错误.
C:由于函数y=2sin(
-x)-cos(
+x)=2sin(
-x)-sin(
-x)=sin(
-x),它的最小值是-1,正确.
D:由函数y=sinπx•cosπx=
sin2πx,它是最小正周期为1的奇函数,故D不正确.
故选C.
B:由x∈[0,
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
函数y=2sin(
| π |
| 6 |
| π |
| 3 |
C:由于函数y=2sin(
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
D:由函数y=sinπx•cosπx=
| 1 |
| 2 |
故选C.
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的周期性与求法,正弦函数的奇偶性,属于中档题.

练习册系列答案
相关题目
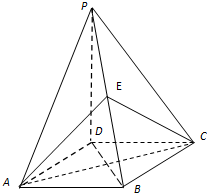 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=