题目内容
 已知三棱锥A-BCD,平面ABD⊥平面BCD,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC.
已知三棱锥A-BCD,平面ABD⊥平面BCD,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC.(1)求证:AB⊥平面ADC;
(2)求三棱锥A-BCD的体积.
分析:(1)根据线面垂直的判定定理,证明AB⊥CD即可.
(2)根据三棱锥的体积公式求出底面积和高即可求体积.
(2)根据三棱锥的体积公式求出底面积和高即可求体积.
解答:解:(1)∵平面ABD⊥平面BCD,DB⊥DC.
∴CD⊥平面ABD,
∵AB?平面ABD,
∴CD⊥AB,
∵AB⊥AD,且AD∩AB=B,
∴AB⊥平面ADC.
(2)取BD的中点O,连结AO,
∵AB=AD=1,AB⊥AD,
∴三角形ABD为等腰直角三角形,
∴A0⊥BD,且AO=
.BD=
.
∵平面ABD⊥平面BCD,A0⊥BD,
∴A0⊥平面BCD,即AO是三棱锥A-BCD的高,
∵DB=DC,DB⊥DC.
∴CD=BD=
,
即三角形BCD的面积为
×
×
=1,
∴三棱锥A-BCD的体积为
×1×
=
.

∴CD⊥平面ABD,
∵AB?平面ABD,
∴CD⊥AB,
∵AB⊥AD,且AD∩AB=B,
∴AB⊥平面ADC.
(2)取BD的中点O,连结AO,
∵AB=AD=1,AB⊥AD,
∴三角形ABD为等腰直角三角形,
∴A0⊥BD,且AO=
| ||
| 2 |
| 2 |
∵平面ABD⊥平面BCD,A0⊥BD,
∴A0⊥平面BCD,即AO是三棱锥A-BCD的高,
∵DB=DC,DB⊥DC.
∴CD=BD=
| 2 |
即三角形BCD的面积为
| 1 |
| 2 |
| 2 |
| 2 |
∴三棱锥A-BCD的体积为
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
点评:本题主要考查线面垂直的判定以及空间三棱锥的体积的计算,要求熟练掌握相应的判定定理和体积公式.

练习册系列答案
相关题目
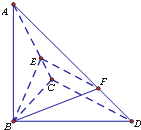 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且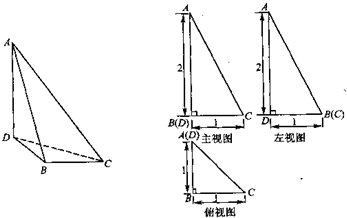 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.