题目内容
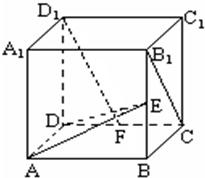 如图,在边长为2的正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点,用向量方法:
如图,在边长为2的正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点,用向量方法:(1)求证:D1F⊥平面ADE;
(2)求CB1与平面ADE所成角的正弦.
分析:(1)由题意,建立空间直角坐标系,利用一条直线与平面里的两条相交直线垂直则该直线就与这一平面垂直的判定定理可以得证;
(2)由题意,利用直线与平面所成角的概念中,利用空间向量中的直线方向向量和平面的法向量之间的关系进而求解.
(2)由题意,利用直线与平面所成角的概念中,利用空间向量中的直线方向向量和平面的法向量之间的关系进而求解.
解答: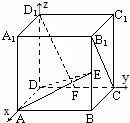 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,
(1)D(0,0,0),A(2,0,0),D1(0,0,2),E(2,2,1),F(0,1,0),
则
=(0,1,-2),
=(2,0,0),
=(0,2,1)
则
•
=0,
⊥
,
•
=0,
⊥
D1F⊥平面ADE;
(2)B1(2,2,2),C(0,2,0),故
=(2,0,2),
•
=(0,0,-4),
|
|=2
,得|
|=
,
设CB1与D1F所成锐角α,则cosα=
=
=
,
CB1与平面ADE所成角β是α的余角,
∴sinβ=cosα=
,
CB1与平面ADE所成角的正弦值是
.
 解:建立如图所示的直角坐标系,
解:建立如图所示的直角坐标系,(1)D(0,0,0),A(2,0,0),D1(0,0,2),E(2,2,1),F(0,1,0),
则
| D1F |
| D A |
| AE |
则
| D1F |
| DA |
| D1F |
| DA |
| D1F |
| AE |
| D1F |
| AE |
D1F⊥平面ADE;
(2)B1(2,2,2),C(0,2,0),故
| CB1 |
| CB1 |
| D1F |
|
| CB1 |
| 2 |
| D1F |
| 5 |
设CB1与D1F所成锐角α,则cosα=
|
| ||||
|
|
| 4 | ||||
2
|
| ||
| 5 |
CB1与平面ADE所成角β是α的余角,
∴sinβ=cosα=
| ||
| 5 |
CB1与平面ADE所成角的正弦值是
| ||
| 5 |
点评:(1)此问重点考查了直线与平面垂直的判定定理用向量的表述得以求证;
(2)此问重点考查了利用空间向量的方法求解直线与平面所成的夹角.
(2)此问重点考查了利用空间向量的方法求解直线与平面所成的夹角.

练习册系列答案
相关题目
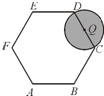 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量