题目内容
A、B是单位圆O上的动点,且A、B分别在第一、二象限.C是圆O与x轴正半轴的交点,△AOB为正三角形.记∠AOC=α.
(1)若A点的坐标为 ,求
,求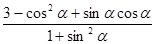 的值;
的值;
(2)求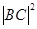 的取值范围.
的取值范围.
(1) 
(2) |BC|2的取值范围是(2,2+ ).
).
解析试题分析:(1)∵A点的坐标为 ,
,
∴tanα= ,
,
(2)设A点的坐标为(cosα,sinα),
∵△AOB为正三角形,
∴B点的坐标为(cos(α+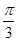 ),sin(α+
),sin(α+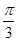 )),且C(1,0),
)),且C(1,0),
∴|BC|2=[cos(α+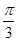 )-1]2+sin2(α+
)-1]2+sin2(α+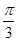 )
)
=2-2cos(α+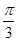 ).
).
而A、B分别在第一、二象限,
∴α∈( ,
,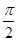 ).
).
∴α+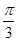 ∈(
∈(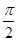 ,
, ),
),
∴cos(α+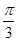 )∈(-
)∈(- ,0).
,0).
∴|BC|2的取值范围是(2,2+ ).
).
考点:三角恒等变换以及三角函数性质
点评:解决的关键是利用三角函数的公式以及三角函数的性质熟练的表示,属于基础题。

练习册系列答案
相关题目
 是△
是△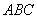 的三个内角,向量
的三个内角,向量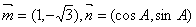 ,且
,且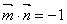
 ;
;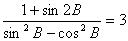 ,求
,求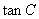 的值。
的值。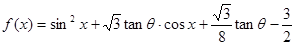 ,其中
,其中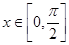 ,
,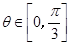
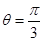 时,求
时,求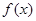 的最大值及相应的
的最大值及相应的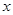 的值;
的值; ,使得函数
,使得函数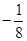 ?若存在,求出对应的
?若存在,求出对应的 .
.  的值.
的值. 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图
,其图象如图
 在
在 的表达式;
的表达式; 的解.
的解.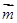 =(
=( sin
sin ,1),
,1),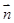 =(cos
=(cos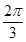 -x)的值;
-x)的值;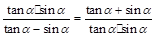 .
. 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为 ,
, ,
,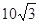 .
.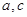 的值;(6分)
的值;(6分)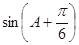 .(4分)
.(4分)
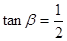 ,求
,求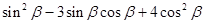 的值.
的值.