题目内容

在中，已知，两边所在的直线分别与轴交于两点，且.

（I）求点的轨迹方程；

（Ⅱ）若，

①试确定点的坐标；

②设是点的轨迹上的动点，猜想的周长最大

时点的位置，并证明你的猜想．

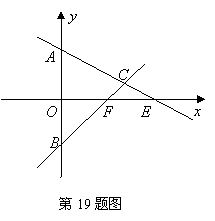
（I）如图，设点，，由三点共线，

，．                …………………2分

同理，由B、C、F三点共线可得 .                 …………………4分

∵，∴,

化简，得点的轨迹方程为.…………………6分（若没有注明则扣1分）

（Ⅱ）若，

①设，

∴.

∴，．

代入， 得．∴，即为椭圆的焦点．  …………………10分

②猜想：取，设是椭圆左焦点，则当点位于直线与椭圆的交点处时，

周长最大，最大值为8．

证明如下：

∴的周长                            …………………14分

练习册系列答案
相关题目
在△ABC中，已知A（0，a），B（0，-a），AC，CB两边所在的直线分别与x轴交于原点同侧的点M，N，且满足|OM|•|ON|=4a2（a为不等于零的常数）
（1）求点C的轨迹方程；
（2）如果存在直线l：y=kx-1（k≠0），使l与点C的轨迹相交于不同的P，Q两点，且|AP|=|AQ|，求a的取值范围．
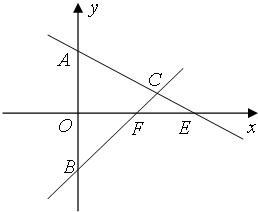精英家教网在△ABC中，已知A（0，1）、B（0，-1），AC、BC两边所在的直线分别与x轴交于E、F两点，且
OE
•
OF
=4．
（I）求点C的轨迹方程；
（Ⅱ）若
BC
=-8
CF
，
①试确定点F的坐标；
②设P是点C的轨迹上的动点，猜想△PBF的周长最大时点P的位置．
在△ABC中，已知A（0，1），B（0，-1），AC、BC两边所在的直线分别与x轴交于E、F两点，且
OE
•
OF
=4．
（1）求点C的轨迹方程；
（2）若
BC
=-8
CF
，
①试确定点F的坐标；
②设P是点C的轨迹上的动点，猜想△PBF的周长最大时点P的位置，并证明你的猜想．

(08年莆田四中一模理)(12分)

在中，已知，，两边所在

的直线分别与轴交于两点，且＝4．

（1）求点的轨迹方程；

（2）若，

①试确定点的坐标；

②设是点的轨迹上的动点，猜想的周长最大时点的位置，并证明你的猜想．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网