题目内容

7．已知在△ABC中，∠C=90°，M是边BC的中点，AC=1．若sinB=$\frac{1}{3}$，则AM=$\sqrt{3}$．

分析 由已知sinB=$\frac{1}{3}$，可求AB，利用勾股定理可求BC的值，进而可求MC，利用勾股定理即可解得AM的值．

解答 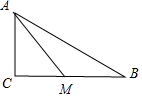解：∵∠C=90°，AC=1．sinB=$\frac{1}{3}$=$\frac{AC}{AB}$=$\frac{1}{AB}$，
∴AB=3，
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$，
∵M是边BC的中点，
∴MC=$\sqrt{2}$，
∴AM=$\sqrt{A{C}^{2}+C{M}^{2}}$=$\sqrt{{1}^{2}+（\sqrt{2}）^{2}}$=$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 本题主要考查了勾股定理，三角函数的定义在解三角形中的应用，考查了数形结合思想和转化思想，属于基础题．

练习册系列答案
相关题目
8．已知△ABC是边长为1的等边三角形，点D，E分别是边AB，BC的中点，连接DE并延长到点F，使得DE=2EF，则$\overrightarrow{AF}$•$\overrightarrow{BC}$的值为$\frac{1}{8}$．
18．等差数列{an}中，其前n项和为Sn，且${S_n}={（\frac{{{a_n}+1}}{2}）^2}$，等比数列{bn}中，其前n项和为Tn，且${T_n}={（\frac{{{b_n}+1}}{2}）^2}$，（n∈N*）
（1）求an，bn；
（2）求{anbn}的前n项和Mn．
15．在数列{an}中，已知a1=1，an+1-an=sin$\frac{（n+1）π}{2}$，记Sn为数列{an}的前n项和，则S2017=1009．
2．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递减，若实数a满足f（log3a）+f（${log_{\frac{1}{3}}}a$）≥2f（1），则a的取值范围是（　　）
A．（0，3]B．（0，$\frac{1}{3}$]C．[$\frac{1}{3}$，3]D．[1，3]
12．定义在R上的函数f（x）满足f（x+2）=f（x），且在区间[-1，1）上，f（x）=$\left\{\begin{array}{l}x-m，-1≤x＜0\\|x-\frac{2}{5}|，0≤x＜1\end{array}$，其中m∈R，若$f（-\frac{5}{2}）=f（\frac{9}{2}）$，则f（5m）=$-\frac{2}{5}$．
19．f（x）=ax2+bx+c（a≠0）．
（Ⅰ）f（x）=x的二实根x1，x2，且0＜x1＜x2＜$\frac{1}{a}$对x∈（0，x1），比较f（x）与x1的大小；
（Ⅱ）若|f（x）|＜1的解集（-1，3），求a的范围．
16．已知曲线y=$\frac{1}{2}$x+sinx，则此曲线在x=$\frac{π}{3}$处的切线方程为6x-6y+3$\sqrt{3}$-π=0．
17．如图，摄影爱好者在某公园A处，发现正前方B处有一立柱，测得顶端O的仰角和立柱底部B的俯角均为30°，已知摄影爱好者的身高约为$\sqrt{3}$米（将眼睛S距地面的距离SA按$\sqrt{3}$米处理）
（1）求摄影爱好者到立柱的水平距离AB和立柱的高度OB
（2）立柱的顶端有一长为2米的彩杆MN，且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转．在彩杆转动的任意时刻，摄影爱好者观察彩杆MN的视角∠MSN是否存在最大值？若存在，求出∠MSN的最大值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网