题目内容
已知函数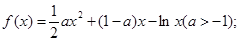
(I)求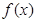 的单调区间;
的单调区间;
(II)若存在 使
使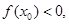 求实数a的范围.
求实数a的范围.
【答案】
(I) 时,单调减区间为(0,1),单调增区间为
时,单调减区间为(0,1),单调增区间为 ;
; 时,单调减区间为
时,单调减区间为 ,单调增区间为
,单调增区间为 .(II)
.(II)
【解析】
试题分析:(I) 首先求函数的导数,然后分 或
或 求出使
求出使 >0或
>0或 <0的区间即可.(II)
存在
<0的区间即可.(II)
存在 使
使 等价于
等价于 ,分
,分 或
或 ,分别求出满足
,分别求出满足 的a的取值即可.
的a的取值即可.
试题解析:函数定义域为
 2分
2分
(I)当 时,
时,
|
|
(0,1) |
1 |
|
|
|
|
|
|
 在(0,1)上递减,
在(0,1)上递减, 上递增 4分
上递增 4分
当 时,
时,
|
|
(0,1) |
1 |
|
|
|
|
|
|
|
|
0 |
|
即 在(0,1),
在(0,1), 递减,在
递减,在 上递增 8分
上递增 8分
(Ⅱ)存在 使
使 等价于
等价于
当 时,
时,
当 l<a<0时,当 时,
时,

则 显然存在
显然存在 使
使 11分
11分
综上, 12分
12分
考点:1.求函数的导数;2.导数的性质;

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目







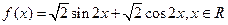 .
.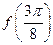 的值;
的值; 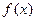 的最大值和最小正周期;
的最大值和最小正周期;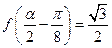 ,
,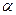 是第二象限的角,求
是第二象限的角,求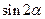 .
. .
.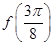 的值;
的值;
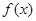 的最大值和最小正周期;
的最大值和最小正周期; ,
,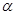 是第二象限的角,求
是第二象限的角,求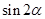 .
.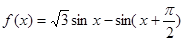 .
.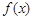 的最小正周期;
的最小正周期;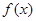 的单调递增区间;
的单调递增区间;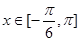 时,求
时,求
 的值;
的值;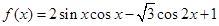 (
(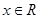 ).
).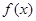 的最小正周期;
的最小正周期;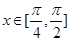 上的最大值和最小值;
上的最大值和最小值;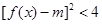 对任意
对任意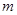 的取值范围.
的取值范围.