题目内容
函数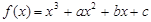 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为
(1)若 在
在 时有极值,求函数
时有极值,求函数 在
在 上的最大值;
上的最大值;
(2)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
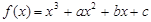 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为
(1)若
 在
在 时有极值,求函数
时有极值,求函数 在
在 上的最大值;
上的最大值;(2)若函数
 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.(1)13(2)b≥0
本试题主要是考查了导数在研究函数中的运用。以及极值的概念和单调性的逆向运用。
(1)因为函数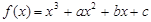 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为 ,若
,若 在
在 时有极值,求导数,然后得到函数
时有极值,求导数,然后得到函数 在
在 上的最大值;
上的最大值;
(2) 上单调递增 又
上单调递增 又

然后对于参数b分类讨论得到结论。
解:(1)




 上最大值为13
上最大值为13
(2) 上单调递增 又
上单调递增 又

 上恒成立.
上恒成立.
①在
②在


③在
综合上述讨论可知,所求参数b取值范围是:b≥0
(1)因为函数
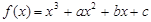 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为 ,若
,若 在
在 时有极值,求导数,然后得到函数
时有极值,求导数,然后得到函数 在
在 上的最大值;
上的最大值;(2)
 上单调递增 又
上单调递增 又

然后对于参数b分类讨论得到结论。
解:(1)


| x |  | -2 |  |  |  |
 | + | 0 | - | 0 | + |
 |  | 极大 |  | 极小 |  |


 上最大值为13
上最大值为13 (2)
 上单调递增 又
上单调递增 又

 上恒成立.
上恒成立.①在

②在



③在

综合上述讨论可知,所求参数b取值范围是:b≥0

练习册系列答案
相关题目
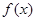 的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=
的图象在点P处的切线方程是y=-x+8,则f(5)+f’(5)=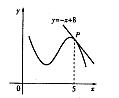
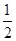
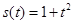 ,则运动开始后4s时物体的动能是( )(其中
,则运动开始后4s时物体的动能是( )(其中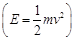 ).
).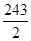 J
J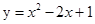 在点(2,2)处的切线方程为
在点(2,2)处的切线方程为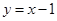
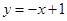
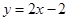

 在点
在点 处的切线方程是
处的切线方程是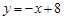 ,则
,则 +
+ = .
= .
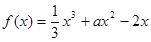 在区间
在区间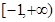 上有极大值和极小值,则实数
上有极大值和极小值,则实数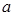 的取值范围是
的取值范围是 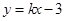 与曲线
与曲线 相切,则实数
相切,则实数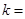 .
. 在
在 处的切线方程为 .
处的切线方程为 .