题目内容
11．某学校新来了五名学生，学校准备把他们分配到甲、乙、丙三个班级，每个班级至少分配一人，其中学生A不分配到甲班的分配方案种数是100．分析 AA的分配方案有2种，若A分配到的班级不再分配其他学生，若A分配到的班级再分配一名学生，若A分配到的班级再分配两名学生，根据分类分步计数原理可得．
解答 解：A的分配方案有2种，若A分配到的班级不再分配其他学生，则把其余四人分组后分配到另外两个班级，分配方法种数是（C43+$\frac{{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$）A22=14；
若A分配到的班级再分配一名学生，则把剩余的三名学生分组后分配到另外两个班级，分配方法种数是C41C31A22=24；
若A分配到的班级再分配两名学生，则剩余的两名学生就分配到另外的两个班级，分配方法种数是C42A22=12．故总数为2×（14+24+12）=100．
故答案为：100．
点评 本题考查计数原理的应用，解题注意优先分析排约束条件多的元素．
练习册系列答案
相关题目
1．已知点P为函数f（x）=lnx的图象上任意一点，点Q为圆[x-（e+$\frac{1}{e}$）]2+y2=1任意一点，则线段PQ的长度的最小值为（ ）
| A． | $\frac{e-\sqrt{{e}^{2}-1}}{e}$ | B． | $\frac{\sqrt{2{e}^{2}+1}-e}{e}$ | C． | $\frac{\sqrt{{e}^{2}+1}-e}{e}$ | D． | e+$\frac{1}{e}$-1 |
2．已知A（1，-2）、B（-1，3），$\overrightarrow{{OA}_{1}}$=4$\overrightarrow{OA}$，$\overrightarrow{{OB}_{1}}$=3$\overrightarrow{OB}$，则$\overrightarrow{{{A}_{1}B}_{1}}$=（ ）
| A． | （8，-6） | B． | （-6，1） | C． | （7，17） | D． | （-7，17） |
19．等差数列{an}的前n项和为Sn，若S2n-1=（2n-1）（2n+1），则Sn=（ ）
| A． | n（n+2） | B． | $\frac{n}{2}$（2n+3） | C． | n（2n+3） | D． | $\frac{n}{2}$（2n+1） |
18．
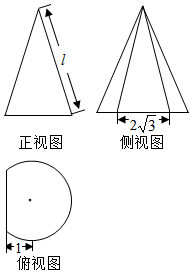如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）| A． | $2\sqrt{2}$ | B． | $2\sqrt{3}$ | C． | 4 | D． | $\sqrt{2}+\sqrt{3}$ |