Question

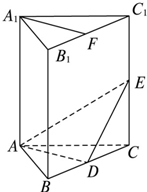如图，在直三棱柱ABC-A₁B₁C₁中，A₁B₁=A₁C₁，D，E分别是棱BC，CC₁上的点（点D不同于点C），且AD⊥DE，F为B₁C₁中点．求证：
（1）平面ADE⊥平面BCC₁B₁；
（2）直线A₁F∥平面ADE．
（3）若E为CC₁中点，且BA=BC=B B₁，求二面角E-AD-C．

Answer 1

分析：（1）依题意，可证AD⊥平面BCC₁B₁，再利用面面垂直的判定定理即可证得平面ADE⊥平面BCC₁B₁；
（2）A₁B₁=A₁C₁，F为B₁C₁的中点，可证A₁F⊥B₁C₁，进一步可证A₁F⊥平面BCC₁B₁；由（1）知AD⊥平面BCC₁B₁，从而A₁F∥AD，利用线面平行的判定定理即可证得结论；
（3）证明∠EDC就是二面角E-AD-C的平面角，即可得出结论．

解答：（1）证明：因为ABC-A₁B₁C₁是直三棱柱，所以CC₁⊥平面ABC．
又AD?平面ABC，所以CC₁⊥AD． 
又因为AD⊥DE，CC₁，DE?平面BCC₁B₁，CC₁∩DE=E，
所以AD⊥平面BCC₁B₁．
又AD?平面ADE，所以平面ADE⊥平面BCC₁B₁．
（2）证明：因为A₁B₁=A₁C₁，F为B₁C₁的中点，所以A₁F⊥B₁C₁．
因为CC₁⊥平面A₁B₁C₁，且A₁F?平面A₁B₁C₁，所以CC₁⊥A₁F，
又因为CC₁，B₁C₁?平面BCC₁B₁，CC₁∩B₁C₁=C₁，所以A₁F⊥平面BCC₁B₁．
由（1）知AD⊥平面BCC₁B₁，所以A₁F∥AD．
又AD?平面ADE，A₁F?平面ADE，所以A₁F∥平面ADE；
（3）解：∵AD⊥平面BCC₁B₁，∴∠EDC就是二面角E-AD-C的平面角．
∵BC=BB₁，E为CC₁中点，D为CB中点，
∴DC=EC，∴∠EDC=45°，
∴二面角E-AD-C的平面角是45°．

点评：本题考查平面与平面垂直的判定，考查直线与平面平行的判定，考查二面角的平面角及求法，考查学生分析解决问题的能力，属于中档题．