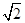题目内容
已 知F1 ,F2分别是双曲线 的左、右焦点,过F1的直线
的左、右焦点,过F1的直线 与双曲线的左、右两支分别交于A、B两点.若ΔABF2是等边三角形,则该双曲线的离心率为
与双曲线的左、右两支分别交于A、B两点.若ΔABF2是等边三角形,则该双曲线的离心率为
A.2
B.
C.
D.
B
解析试题分析:
如图依题意可得 .又因为
.又因为 .所以
.所以 .又因为
.又因为 .所以
.所以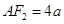 .即在三角形
.即在三角形 .由余弦定理可得
.由余弦定理可得 .所以离心率为
.所以离心率为 .
.
考点:1.双曲线的性质.2.解三角形的知识.3.双曲线的定义.4.待定系数的思想方法.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
设双曲线 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,
, 是
是 上的点,
上的点, ,
, ,则
,则 的离心率为
的离心率为
A. | B. | C.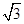 | D. |
对于任意给定的实数 ,直线
,直线 与双曲线
与双曲线 ,
,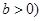 最多有一个交点,则双曲线的离心率等于( )
最多有一个交点,则双曲线的离心率等于( )
A. | B. | C. | D. |
若抛物线 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C.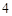 | D. |
椭圆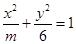 的焦距为2,则m的取值是 ( )
的焦距为2,则m的取值是 ( )
| A.7 | B.5 | C.5或7 | D.10 |
下列双曲线中,有一个焦点在抛物线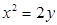 准线上的是( )
准线上的是( )
A. | B. |
C. | D. |
 的两个焦点及虚轴的两个端点为顶点的四边形中,有一个内角为
的两个焦点及虚轴的两个端点为顶点的四边形中,有一个内角为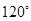 ,则双曲线
,则双曲线




 与双曲线
与双曲线 在交点处正交,则椭圆
在交点处正交,则椭圆



 (a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为()
(a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为()