题目内容
∫01exdx与∫01ex 2dx相比有关系式( )
| A、∫01exdx<∫01ex 2dx | B、∫01exdx>∫01ex 2dx | C、(∫01exdx)2=∫01ex 2dx | D、∫01exdx=∫01ex 2dx |
分析:根据积分所表示的几何意义是以直线x=0,x=1及函数y=ex或y=ex 2在图象第一象限内圆弧与坐标轴围成的面积,只需画出函数图象观察面积大小即可.
解答: 解:∫01exdx表示的几何意义是以直线x=0,x=1及函数y=ex在图象第一象限内圆弧与坐标轴围成的面积,
解:∫01exdx表示的几何意义是以直线x=0,x=1及函数y=ex在图象第一象限内圆弧与坐标轴围成的面积,
∫01ex 2dx表示的几何意义是以直线x=0,x=1及函数y=ex 2在图象第一象限内圆弧与坐标轴围成的面积,
如图
∵当0<x<1时,exx>ex 2,故有:∫01exdx>∫01ex 2dx
故选B.
 解:∫01exdx表示的几何意义是以直线x=0,x=1及函数y=ex在图象第一象限内圆弧与坐标轴围成的面积,
解:∫01exdx表示的几何意义是以直线x=0,x=1及函数y=ex在图象第一象限内圆弧与坐标轴围成的面积,∫01ex 2dx表示的几何意义是以直线x=0,x=1及函数y=ex 2在图象第一象限内圆弧与坐标轴围成的面积,
如图
∵当0<x<1时,exx>ex 2,故有:∫01exdx>∫01ex 2dx
故选B.
点评:本题主要考查了定积分,定积分运算是求导的逆运算,解题的关键是求原函数,也可利用几何意义进行求解,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题正确的是( )
| A、单位向量都相等 | ||||||||||||
B、若
| ||||||||||||
C、若|
| ||||||||||||
D、若
|
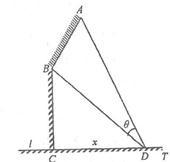 如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60°(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4