Question

【题目】是边长为的等边三角形，E、F分别为AB、AC的中点，，沿EF把折起，使点A翻折到点P的位置，连接PB、PC，则四棱锥的外接球的表面积的最小值为________，此时四棱锥的体积为________.

Answer 1

【答案】

【解析】

根据题意，当梯形BCEF的外接圆的圆心为四棱锥的外接球的球心时，外接球的半径最小，易得BC的中点即为梯形的外接圆圆心，也即为四棱锥的球心，进而求解.

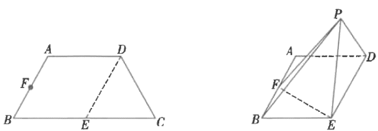
如图所示：

四边形BCEF为梯形，则必有外接圆，设O为梯形BCEF的外接圆的圆心，即为外接球的球心时，外接球的半径最小，也就使得外接球的表面积最小，过A作BC的垂线交BC于点M，交EF于点N，连接PM，PN，点O必在AM上，

因为E，F，分别为中点，

所以，

所以，即是直角三角形，

因为是边长为的等边三角形，E、F分别为AB、AC的中点，

所以,

所以点M为为梯形BCEF的外接圆的圆心，即点O与点M重合,

所以，,

所以四棱锥的高为：,

所以棱锥的外接球的表面积的最小值为，

此时四棱锥的体积为.

故答案为：(1). (2).