题目内容
设数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上,
上, 为常数,
为常数, .
.
(Ⅰ)求 ;
;
(Ⅱ)若数列 的公比
的公比 ,数列
,数列 满足
满足 ,求证:
,求证: 为等差数列,并求
为等差数列,并求 ;
;
(III)设数列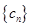 满足
满足 ,
, 为数列
为数列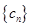 的前
的前 项和,且存在实数
项和,且存在实数 满足
满足 ,
, ,求
,求 的最大值.
的最大值.
【答案】
(1)
(2)略
(3)
【解析】解:(Ⅰ)由题设, ①………………1分
①………………1分

由①, 时,
时,
① ②得,
②得,

 …………………………………………………………4分
…………………………………………………………4分
(Ⅱ)由(Ⅰ)知
化简得:  …………………………6分
…………………………6分
 为等差数列,
为等差数列,
 …………………………………………………………………8分
…………………………………………………………………8分
(III)由(Ⅱ)知 [
[
 为数列
为数列 的前
的前 项和,因为
项和,因为 ,
,
所以 是递增的,
是递增的,  .………………………………………10分
.………………………………………10分
所以要满足 ,
, ,
,
所以 的最大值是
的最大值是 .……………………………………
.……………………………………

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
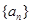 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图像上.
的图像上. ,
, 是数列
是数列 的前
的前 对所有
对所有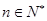 都成立的最小正整数
都成立的最小正整数 .
. 的前
的前 项和为
项和为 ,点
,点 在直线
在直线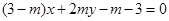 上,
上, 为常数,
为常数, .
. ;
; ,数列
,数列 满足
满足 ,求证:
,求证: 为等差数列,并求
为等差数列,并求 ;
; 满足
满足 ,
, 为数列
为数列 满足
满足 ,
, ,求
,求 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上,(
上,( 为常数,
为常数, ,
,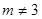 ).
). ;
;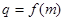 ,数列
,数列 满足
满足 ,
, ,
, ,求证:
,求证: 为等差数列,并求
为等差数列,并求 ;
; 满足
满足 ,
, 为数列
为数列 满足
满足
 ,求
,求 的前
的前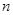 项和为
项和为 ,点
,点 在直线
在直线 上,
上, 为常数,
为常数, .
. ;
; ,数列
,数列 满足
满足 ,求证:
,求证: 为等差数列,并求
为等差数列,并求 ;
; 满足
满足 ,
, 为数列
为数列 满足
满足 ,
, ,求
,求