题目内容
在如图所示的锐角三角形空地中，欲建一个面积最大的内接矩形花园（阴影部分），则其边长x为
- A.35m
- B.30m
- C.25m
- D.20m
D
分析：设矩形高为y，由三角形相似可求得40=x+y结合x＞0，y＞0，x＜40，y＜40，利用基本不等式即可求得答案．
解答：设矩形高为y，由三角形相似得：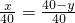
，
且x＞0，y＞0，x＜40，y＜40，变形可得x+y=40
故矩形的面积S=xy≤
=400
当且仅当x=y=20m时，取等号，
故选D
点评：本题考查函数的最值，基本不等式，考查相似三角形的应用，求得40=x+y是关键，属中档题．
分析：设矩形高为y，由三角形相似可求得40=x+y结合x＞0，y＞0，x＜40，y＜40，利用基本不等式即可求得答案．
解答：设矩形高为y，由三角形相似得：
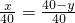，且x＞0，y＞0，x＜40，y＜40，变形可得x+y=40
故矩形的面积S=xy≤
=400当且仅当x=y=20m时，取等号，
故选D
点评：本题考查函数的最值，基本不等式，考查相似三角形的应用，求得40=x+y是关键，属中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
有两个实数根，则实数k的取值范围是________．
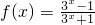，判断函数f（x）的奇偶性，并说明理由．
=3，求a+a-1；
，f（-2）=10，求f（2）．
}，N={（x，y）|y=x+m}，且M∩N≠∅，则m的取值范围为________．