题目内容
在△ABC中, .
.
(I)求∠C的大小;
(II)若AB=1,求△ABC周长的取值范围.
解:(I)由tan =2sinC,
=2sinC,
∴
∵0< >0,
>0,
∴sin2 .
.
∴
(II)由正弦定理,得 ,
,
△ABC的周长y=AB+BC+CA=1+ -A)
-A)
=
= ),
),
∵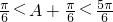 ,
,
∴ )≤1,
)≤1,
所以,△ABC周长的取值范围是(2,3)
(I)利用三角形的三角和为π及三角函数的诱导公式化简已知的等式,利用三角形中内角的范围,求出∠C的大小
(II)利用三角形的正弦定理将边BC,CA用角A的三角函数表示,利用两角差的正弦公式展开,再利用三角函数中的公式
 将三角形的周长化简成y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出△ABC周长的取值范围.
将三角形的周长化简成y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出△ABC周长的取值范围.
点评:解决三角函数的取值范围问题一般利用三角函数的诱导公式、两个角的和、差公式、倍角公式以及公式 将三角函数化为y=Asin(ωx+φ)+k形式.
将三角函数化为y=Asin(ωx+φ)+k形式.
 =2sinC,
=2sinC,∴

∵0<
 >0,
>0,∴sin2
 .
.∴

(II)由正弦定理,得
 ,
,△ABC的周长y=AB+BC+CA=1+
 -A)
-A)=

=
 ),
),∵
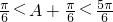 ,
,∴
 )≤1,
)≤1,所以,△ABC周长的取值范围是(2,3)
(I)利用三角形的三角和为π及三角函数的诱导公式化简已知的等式,利用三角形中内角的范围,求出∠C的大小
(II)利用三角形的正弦定理将边BC,CA用角A的三角函数表示,利用两角差的正弦公式展开,再利用三角函数中的公式
 将三角形的周长化简成y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出△ABC周长的取值范围.
将三角形的周长化简成y=Asin(ωx+φ)+k形式,利用三角函数的有界性求出△ABC周长的取值范围.点评:解决三角函数的取值范围问题一般利用三角函数的诱导公式、两个角的和、差公式、倍角公式以及公式
 将三角函数化为y=Asin(ωx+φ)+k形式.
将三角函数化为y=Asin(ωx+φ)+k形式. 
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 ABC中,
ABC中, , sinB=
, sinB= .
. ,求
,求 ABC中,
ABC中, ,
sinB=
,
sinB= .
. ,求
,求