题目内容
已知定义在R上的函数 
,其中函数
的图象是一条连续曲线，则方程
在下面哪个范围内必有实数根（ ）
| A．(0,1) | B．(1,2) | C．(2,3) | D．(3,4) |
C
解析试题分析：方程的根可以转化成函数的零点:判断的主要方法是利用根的存在性定理，判断连续函数在给定区间端点处的符号是否相反.
由题中有抽象函数
连续,所以使其系数为0即可不求其解析式,即
得
可验证
故选C
考点：函数零点的判定.
练习册系列答案
中考解读考点精练系列答案
相关题目
已知
，且
，
，则
等于
A． | B． | C． | D． |
已知函数
，则
（ ）
A． | B． | C． | D． |
设
表示不大于
的最大整数，则函数
＝lg2x－[lgx]－2的零点个数( )个
| A．1 | B．2 | C．3 | D．4 |
已知
，那么
用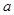
表示是（ ）
A． | B． | C． | D． |
已知函数
则
等于 （ ）
A． | B． | C． | D． |
等比数列
的各项均为正数,且
,则
( )
| A．12 | B．10 | C．8 | D． |
函数
的零点所在的大致区间是( )
| A．(0，1) | B．(1，2) | C．(2，3) | D．(3，4) |
(
,
为自然对数的底数).若曲线
上存在
使得
,则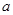
的取值范围是( )
