题目内容
(本小题满分12分)已知函数 的图象过点
的图象过点 ,且点
,且点
 在函数
在函数 的图象上.
的图象上.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,若数列
,若数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
(1) (
( ),(2)见解析
),(2)见解析
【解析】
试题分析:由条件函数 的图象过点
的图象过点 ,利用待定系数法求
,利用待定系数法求 即可,第二步利用错位相减法求数列的和,得到
即可,第二步利用错位相减法求数列的和,得到
试题解析:(1)由条件函数 的图象过点
的图象过点 ,知:
,知: ,所以:
,所以: ,
,
 过点
过点 ,所以:
,所以: ,则:
,则:

(2)





所以:
考点:1.待定系数法;2.数列求和(错位相减法);
考点分析: 考点1:函数的图像 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.
 ;
; .
.
 B.
B. C.
C. D.
D.
 ,则该锥体的俯视图可以是( )
,则该锥体的俯视图可以是( )

 ,若
,若 ,则实数
,则实数 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,且
,且 ,则正整数
,则正整数 为 .
为 .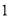 的等边
的等边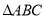 中,
中,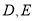 分别在边BC与AC上,且
分别在边BC与AC上,且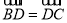 ,
,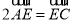
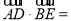 ( )
( )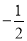 B.
B. 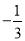 C.
C.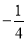 D.
D.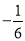
 ,若方程
,若方程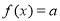 有四个不同的解
有四个不同的解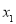 ,
,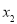 ,
, ,
,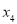 ,且
,且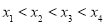 ,则
,则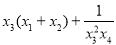 的取值范围是( )
的取值范围是( )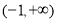 B.
B.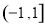 C.
C.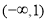 D.
D.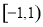
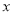 ,
, 满足
满足 ,若目标函数
,若目标函数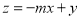 的最大值为
的最大值为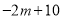 ,最小值为
,最小值为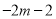 ,则实数
,则实数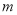 的取值范围是 .
的取值范围是 .