题目内容
已知幂函数y=f(x)的图象过点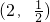 ,求出此函数的解析式,并判断并证明f(x)的奇偶性.
,求出此函数的解析式,并判断并证明f(x)的奇偶性.
解:设f(x)=xa
将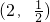 代入得
代入得 (2分)
(2分)
解方程得:a=-1,
∴ (4分)
(4分)
定义域为{x|x≠0}(5分)
∵ ,
,
∴f(x)为奇函数(8分)
分析:根据幂函数的概念设f(x)=xa,将点的坐标代入即可求得a值,从而求得函数解析式.要判断函数的奇偶性我们可以根据函数奇偶性的定义判断函数的奇偶性.
点评:解答本题关键是待定系数法求幂函数解析式、指数方程的解法等知识,本题考查的知识点是奇(偶)函数性.
将
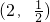 代入得
代入得 (2分)
(2分)解方程得:a=-1,
∴
 (4分)
(4分)定义域为{x|x≠0}(5分)
∵
 ,
,∴f(x)为奇函数(8分)
分析:根据幂函数的概念设f(x)=xa,将点的坐标代入即可求得a值,从而求得函数解析式.要判断函数的奇偶性我们可以根据函数奇偶性的定义判断函数的奇偶性.
点评:解答本题关键是待定系数法求幂函数解析式、指数方程的解法等知识,本题考查的知识点是奇(偶)函数性.

练习册系列答案
相关题目