题目内容
数列 的前
的前 项和
项和 满足
满足 (
( ,且
,且 ).数列
).数列 满足
满足 .
.
(Ⅰ)求数列 的前
的前 项和
项和 ;
;
(Ⅱ)若对一切 都有
都有 ,求
,求 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2) .
.
【解析】本试题主要考察了数列的前n项和与其通项公式的关系的运用,以及证明数列的单调性的综合运用。
解:(Ⅰ)当 时
时 ,
,  解得
解得

当 ≥2时
≥2时  …………2分
…………2分

 ,
,
 ,两式相减得
,两式相减得


所以数列 是首项为
是首项为 ,公比为
,公比为 的等比数列
的等比数列

从而

 ……
…… =
=
设 ……+
……+ ,则
,则

 ……+
……+
 ,
,




(Ⅱ)由 可得
可得
① 当 时,由
时,由 可得
可得 ,
,

 对一切
对一切 都成立,
都成立, 此时的解为
此时的解为 .
.
② 当 时,由
时,由 可得
可得

 ≥
≥

 对一切
对一切 都成立,
都成立,

 .
.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 的前
的前 项和
项和 满足
满足 ,其中
,其中 .
. ,求
,求 及
及 ;
;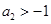 ,求证:
,求证: ,并给出等号成立的充要条件.
,并给出等号成立的充要条件. 中,数列的前
中,数列的前 项和
项和 满足
满足 .
. ;
;